COSMOLOGIA ARCAICA
Sezione Indiana

Due ninfe indiane, Apsara, in un tempietto a Kali, a Siliserh
La revisione del pitagorismo nella cultura indiana
° °
° ° °
° ° ° °
Il significato astronomico della tetraktys viene colto se si passa dalla studio dei rapporti a quello delle successioni, di cui quella geometrica veniva considerata la principale. Nella successione aritmetica dei primi quattro numeri, cominciante dall'unità, si trova un'unica progressione geometrica:
il cui significato astronomico è legato alla scoperta molto antica della precessione degli equinozi, conosciuta sotto la forma di un movimento del polo celeste lungo una circonferenza con il centro costituito dal polo dell'eclittica.
Il che implica che ad 1° corrispondono 72 anni e 1 rivoluzione dei nodi lunari è pari a 18.6 anni. La precessione, il cui simbolo è dato dalla svastica, comporta la distinzione dell'anno sidereo dall'anno tropico, il primo essendo il tempo per il ritorno del sole al medesimo punto della sfera celeste e il secondo, il tempo per il ritorno del sole ai medesimi punti equinoziali o solstiziali. Ciò che è difficile da misurare ed esprimere è la differenza, che nella cultura arcaica veniva chiamata Fulmine e nelle varie tradizioni religiose si accompagnava sempre con qualche divinità, che c'è tra l'anno sidereo e l'anno tropico. Questa differenza, per il medesimo tempo di quattro rivoluzioni dei nodi e di 1° 2' di arco del polo sul percorso della precessione, è con buona approssimazione pari a:
formula facilmente memorizzabile. Si può ricordare che 496 è un numero perfetto,secondola definizione euclidea, ed è ad esso che Platone si riferisce in un passo della Repubblica
Per la completa derminazione del tempo e del ciclo lunisolare è necessario sapere di quanto l'anno di 365.25 giorni supera l'anno tropico e quanti mesi sinodici medi della luna vi siano in 72 anni, ovvero per 1° di precessione.
La prima relazione si trova nella equivalenza che in 10000 anni, quella differenza che veniva chiamata tuono, ammonta a 78 giorni, cioè al numero triangolare di lato 12, cioè la somma di 1+2+3+...12 = 78.
La seconda relazione determina il numero dei mesi sinodici della luna per 72 anni in:
Ora, se invece di sottrare un giorno si sottrae una quantità maggiore, il periodo sinodico della luna diminuisce o aumenta secondo un determinato rapporto: per 61/60 diminuisce e per 60/61 aumenta. Sicchè per 60° di precessione, per 4320 anni, i mesi lunari saranno:
Ora con tre rapporti numerici, uno per la differenza dell'anno sidereo dall'anno tropico, l'altro per la differenza dell'anno giuliano dall'anno tropico e il terzo superiore all'unità per il periodo sinodico della luna, viene determinata completamente la struttura della Cosmologia arcaica.
La teoria musicale indiana prevedeva fin dall'antichità una complessa organizzazione della scala, e i nomi all'interno della scala, indicano in primo luogo distanze e non note. Le distanze erano tutte suddivise: i semitoni in due elementi, ed i toni interi in tre o quattro ciascuno, in tutto ventidue elementi o srutis:
3 2 4 4 3 2 4
9 4 9
22
Siamo ora in grado di riconoscere nello schema indiano relativo al Giorno di Brahma la revisione del sistema conosciuto sotto la tradizione pitagorica.
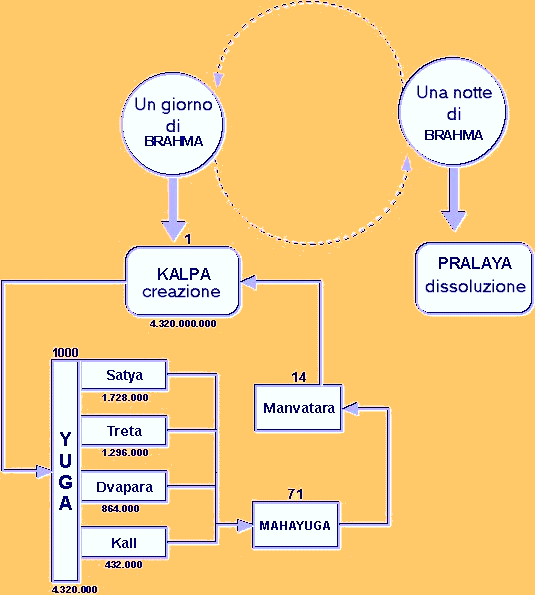
Assunto come unità 432.000 anni i quattro periodi in cui è suddiviso l'intero Giorno corrispondono ad 1,2,3,4 volte l'unità, sicché l'intero ciclo da prendersi in considerazione è quello che sta in rapporto all'intero ciclo della precessione di 360° nel rapporto di 3/2 secondo un intervallo della scala musicale. Ne deriva che sono ben 10 cicli di 4320 anni, essendo questo relativo a 60°. Se in 4320 anni tropici vi sono 53431 mesi nel ciclo totale che prendiamo in esame, i mesi lunari saranno 534310, un numero divisibile per 14. Sicchè ogni Manvatara comprendono 38165 mesi.
L'eventuale revisione non può essere fatta su qualcosa di osservabile, ma sul parametro fondamentale. che è quello relativo alla corrispondenza di 72 anni per 1°. Di quanto è inferiore a 72 anni oppure di quanto è superiore a 71 anni? Se il tutto è suddiviso in 14 parti, si tratta di sapere il numero delle parti da aggiungere a 71. Nello schema deve essere indicato come totale la parte in 14mi da aggiungere a 71 oppurre da sottrarre a 72.
50".4 come misura annuale della precessione,
precisamente quella della cosmologia indù.
 relativo al periodo sinodico della luna, del rapporto per la differenza dell'anno sidereo dall'anno tropico (Fulmine= Indra?) e quello della differenza dell'anno di 365.25 giorni dall'anno tropico (tuono).
relativo al periodo sinodico della luna, del rapporto per la differenza dell'anno sidereo dall'anno tropico (Fulmine= Indra?) e quello della differenza dell'anno di 365.25 giorni dall'anno tropico (tuono).A titolo puramente indicativo, in mancanza di altri elementi, i parametri del sistema compatili con le ipotesi premesse sono indicati nella presente tabella. I tre rapporti sono 38165/6444 per la quantità x da sottrarre alla relazione che lega 72 anni anni "giuliani" al numero dei mesi sinodici, 5/352 per il fulmine, cioè in 352 anni la differenza tra l'anno sidereo e l'anno tropico ammonta a 5 giorni, e per il tuono il rapporto implica che in 640 anni la differenza sia di 5 giorni. Si noti la coincidenza, astronomicamente non significativa, che la somma di 352 e di 640 sia proprio il tempo necessario (992 anni) affinchè la differenza tra l'anno sidereo e l'anno tropico sia di 14 giorni, secondo i parametri del sistema derivante dalla tetraktys pitagorica e che il loro rapporto sia di 11/20.
Nella tabella sono riportati i conseguenti periodi lunari e solari. Viene indicata per quei parametri la misura annuale della precessione e il termine correttivo per la longitudine del sole sull'arco veloce alla fine del ciclo di 53431 mesi.
Nel sito di Dwight William Johnson, tecnicamente accurato per il calcolo astronomico e l'analisi del sistema, Exegesis of Hindu Cosmological Time Cycles viene data una tabella di confronto tra i parametri della cosmologia indù e quelli che l'astronomo Newcomb calcolò per il 1 gennaio 1900 d.C.

L'aver assunto come base questo intervallo di tempo non implica affatto una serie costante di osservazioni e di registrazioni, ma la ragione che esso facilita una serie di calcoli. Che il tempo totale comprenda 10 di questi cicli, cioè sia di 43.200 anni, è legato al fatto che, assunto come prima approssimazione 22/7 il rapporto della circonferenza al diametro, presente nella teoria musicale indiana con la suddivisione dell'ottava in 22 shrutis e in 7 note, si trova che:
© 2001 Proprietà letteraria riservata