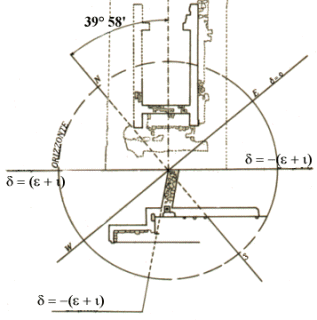
Nel precedente studio abbiamo  già mostrata la connessione tra l’orientamento del tempio maggiore e ciò che viene precisamente detto nel proemio. L’orientamento del tempio permette di individuare quando ciclicamente avviene quell’evento descritto nei vv.15-21. Infatti  prolungando fino all’orizzonte la linea dello stereobate verso sud-est si trova il punto  in cui la luna sorge avendo la massima declinazione sud. La linea degli equinozi è approssimativamente la bisettrice dell’angolo formato dal precedente muro poligonale e dallo stereobate, come si può vedere nella pianta del tempio. L’angolo di 39° 58’ è l’angolo di amplitudine ortiva ed occasa della Luna quando essa raggiunge la massima declinazione nord e sud.

<

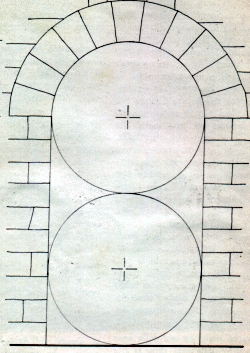
raggio =1(m. 1,34)

larghezza = 2(m. 2,68)

altezza muro = 3(m. 4,02)

altezza interna = 4(m. 5,36)

per cui la luce dell’arco iscrive esattamente due circonferenze l’una sull’altra e tangenti tra di loro, aventi per diametro la larghezza.” (8).

Si può vedere che il modulo costruttivo di Porta Rosa è strutturato sulla sequenza della tetraktys pitagorica.

Fig. 6 La struttura di Porta Rosa . Da M. Napoli, op.cit., pag.27

Inoltre, ponendoci sulla linea del contrafforte di sinistra (fig.4), distante 12 m. dalla porta, lunga 7.72 m (Fig.7) si può calcolare l’altezza massima di un astro (5,36/19,72 =  sin (90° -d )  con d la declinazione dell’astro, quando passa internamente tangente all’arco. L’altezza massima del Sole al solstizio invernale è approssimativamente di 26° 32’ al tempo di Parmenide.

                                                               5,92 x tg (73.29) = 19.72

quanto misura in metri  tutto il complesso monumentale della Porta Rosa dal muro di contenimento (Fig.7). Queste

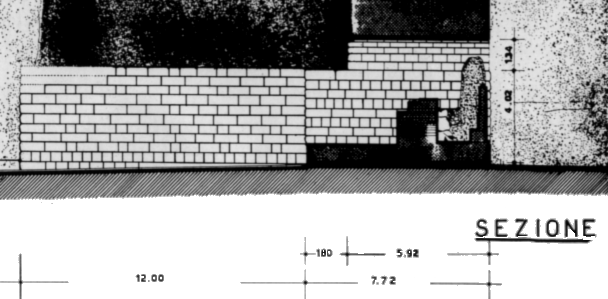
Fig. 7 Pianta della Porta Rosa . Da Mario Napoli, op.cit., pag.25.

semplici osservazioni mostrano come non sia arbitrario ritenere che questo monumento, così caratteristico a Velia, sia in relazione ad un sapere astronomico e ad una modalità progettuale derivata dalla attività di Parmenide di sistematica osservazione dei moti solari e lunari, espressamente indicata nel proemio.

 Si può ancora facilmente rilevare (fig. 4) come l’arco inferiore della porta, sia composto di undici conci radiali e quello superiore in funzione di arco di scarico di tredici. La funzione dell’arco superiore, posteriore alla porta, è eminentemente statica  e non faceva parte del progetto originario a quanto è dato di sapere.

 Nel proemio il  termine porte compare al verso 11 e viene indirettamente menzionato al verso 13. Con queste due occorrenze si trova la seguente sequenza significativa : il primo valore è 11, il secondo è la somma di 11 e 13, e il terzo valore è la somma dei primi due.  In tal modo si trova il numero dei mesi trascorsi dalla precedente origine.

                Dato dunque un  intervallo di 11,24,35 mesi,  l’operazione To + 11,24,35 mesi individua l’origine arcaica greca. Da questa origine si deve calcolare l’intervallo di 3,17,4 mesi dato dalle differenze successive delle occorrenze del termine cavalle. Gli eventi descritti nel proemio sono posteriori e si giunge con Parmenide alla casa della dea mediante l’individuazione degli eventi e del loro significato per il sapere astronomico.

                C’è una perfetta coincidenza a quanto abbiamo trovato in un precedente studio sul mito di Apollo rappresentato nel riquadro di una anfora (9) e a quanto ci è risultato nell’analisi del frammento di Petrone d’Imera (10). Si giunge infatti  al 510 a. c. e precisamente al 27 marzo, ad un plenilunio con il Sole vicinissimo al punto vernale. Questa informazione, tuttavia, non si ritrova direttamente nel testo. D’altra parte il lettore contemporaneo di Parmenide avrebbe immediatamente riconosciuto il riferimento ad un tempo che era comune. Per la lettura verrà impiegata questa notizia , cioè che il Sole si trova all’equinozio durante quel plenilunio, unicamente per un controllo e vedremo come Parmenide dia la necessaria informazione di longitudine che permette di calcolare con il sistema arcaico la posizione del Sole al plenilunio del 27 marzo 510 a.C. , indicato dopo che sono passati 3,17,4 mesi secondo il proemio.

La struttura delle occorrenze del proemio Fr.I,1-28

I termini delle occorrenze sono i seguenti: porte, cavalle, carro, fanciulle, via, dea, aurighe, casa, Dike

1                                                Cavalle,

2                                                via

…..

4                                                                                                …….  cavalle 

5                                                carro ….fanciulle …via.

…….

…….

 …..

9                                                … fanciulle …..,

 …..

11                                              ….. porte …..

…..

13                                              .. le medesime (porte) …

14                                              ….                Dike …..

15                                              …..                 fanciulle ….

------

……

-----

-----

----

21                                                le fanciulle ………………... carro e  cavalle  .

22                                              E la dea …..

…..

24                                              ……  aurighe  immortali,

25                                              cavalle  …..

….

27                                              ….. via…..

28                  ……  Dike.

La struttura delle occorrenze è dunque la seguente:

cavalle (1,4,21,25); via (2,5,27); carro (5,21), fanciulle (5,9,15,21); porte (11,13); Dike (14,28); dea (22) ; casa (25)

La Dea e le Aurighe immortali. vv.22-24

E la dea benevola mi accolse, con la mano destra

la mia destra prese, e così rivolgendomi la parola disse:

O giovane, degno compagno di aurighe immortali,

Prima di tutto cerchiamo di leggere l’informazione decisiva sulla dea e sulle aurighe immortali, di cui il giovane Parmenide  è un degno compagno.  Si tratta di cercare una longitudine. La  dea è in rapporto alla più luminosa stella ed è per antonomasia la dea o la divina in diverse culture, anche se il nome cultuale è diverso nelle diverse tradizioni culturali e religiose.

Per l’occorrenza al v.22 del termine dea, essendo posto subito dopo l’intervallo di (21-4) delle due centrali occorrenze di  cavalle, il primo termine della sequenza significativa  per la dea  è 17 e il secondo (22-17), e il terzo zero. D’altra parte l’ascoltatore colto già conosceva il possibile valore per la dea per il tempo indicato dalle differenze successive delle occorrenze di cavalle. Questo implica che la longitudine di Sirio al tempo zero in Gemelli corrisponde all’arco di precessione per il tempo di 2,23,21 mesi e al tempo indicato nel proemio a quello di 17,5,0 mesi. Già nell’analisi di altri testi abbiamo incontrato questo valore per Sirio.

Le aurighe immortali sono due stelle della costellazione dell’Auriga, l’alfa e beta, ed hanno una particolarissima funzione nella cultura arcaica. Infatti la loro differenza in longitudine trasformata in anni solari e in mesi fornisce la base di un ciclo lunisolare, ciclo conosciuto sotto il nome della Fenice (Dante, Inferno,XXIV,107; 107x60+24=6444) e sotto l’età del cervo (Esiodo). Fu impiegato nell' 1800 da astronomi per la ricerca delle eclissi, come si può vedere nella  cronologia astronomica del Ginzel (11) . Esso si ritrova nel riquadro dell’incontro di Apollo e Artemide su di un’anfora cicladica ritrovata a Milo, come abbiamo già mostrato (12). Le due stelle dell’Auriga  sono ben presenti nella cultura elamita sotto il nome dell’Ibex. Quando b Aur misura in longitudine il tempo espresso in anni, 521 diviso per 72, la longitudine di Capella segna l’equinozio di primavera. Se si congiunge b Aur con la q si trova addirittura la intersezione dell’equatore galattico con l’eclittica, si trova quella confluenza dei fiumi, narrata sia nel Gilgames che in una Sura del Corano.  Il che significa che la longitudine di b Aur indica la longitudine di quella intersezione. Per la latitudine di Velia al tempo di Parmenide si deve ancora ricordare che la stella culmina al meridiano vicinissima allo zenith, vicinissima alla sede della Demone.

Per l’occorrenza al v. 24  delle aurighe immortali, ci si deve domandare perché la dea qualifichi il giovane Parmenide degno compagno delle aurighe.  La ragione di tale rilievo da parte della dea riposa sul fatto che Parmenide impiega il ciclo di 521 anni per calcolare la longitudine del Sole e della Luna. Senza questa informazione sulle due stelle non siamo in grado di controllare quanto Parmenide racconta. Per il ciclo dato dalla differenza di longitudine delle due stelle la sequenza numerica è la seguente:

                                (24-17)° (17-3)’ (24-14)” = 7° 14’ 10”  =  521/72

Nel ciclo di 521 anni pari a 6444 mesi lunari, i punti di discontinuità si trovano a 142° di longitudine e a 342°.  Nell’arco dal primo al secondo il Sole percorre 30° ogni mese lunare, mentre dal secondo al primo, trovandosi sull’arco più breve e più lento,  percorre   30° x 521/557 ogni mese lunare, cioè 28° 3’ 40” al mese.

Il riferimento alla galassia  del Fr. 11 suggerisce che si debba cercare anche la longitudine di b Aur  e non solo la sua differenza da Capella. Data la sequenza 3,17,4  al tempo indicato da questa sequenza la longitudine di b Aur è

                                                (17-4), (13 + 17-3), (17-3) mesi = 13,27,14 mesi

Al tempo segnato da

Il cerchio come simbolo della dea

Poiché il termine dea è al verso 22 e il termine casa al verso 25, il diametro misura  3,1,49 + 22+25,22 = 3, 49,11 unità, cioè 13751 unità. Al verso 13751 della Divina Commedia di Dante occorre il termine circunferenza (Paradiso,XXX,104). Prestigiosa corrispondenza del sapere in autori così lontani nel tempo, ma che appartengono ancora per vie diverse alla medesima tradizione del sapere arcaico anche per quanto concerne la sua comunicazione. Alla precedente domanda se ne aggiunge un’altra e riguarda l’occorrenza di questo termine numerico (13751) in un ipotetico catalogo stellare, frutto non di osservazione individuale ma di trasmissione tradizionale mediante racconti.  Al tempo zero in Gemelli quale stella aveva come longitudine l’arco di precessione corrispondente a 13751 mesi? Con un breve controllo si può rispondere che la stella più probabile è a Geminorum, cioè Castore, dato che l’equinozio si trova tra m e h  Geminorum. Tuttavia il rapporto costante di circonferenza e diametro che noi chiamiamo p (il cuore immobile della verità ben rotonda?) legato alla dea non è questo, dipendendo dalla longitudine iniziale espressa in mesi della stella dei Gemelli. Da esso possiamo agevolmente derivare il nuovo rapporto, conoscendo la longitudine iniziale di Sirio, a cui la dea senza identificarsi è legata, essendo essa  la struttura del sapere connessa alla stella, come Apollo non è banalmente il Sole, ma il sistema di guida del Sole. Si può inoltre osservare che la relazione di Sirio a Castore, o meglio la relazione che Sirio intrattiene con ‘13751’ è data anche dal fatto che una circonferenza con un raggio di 21600 unità ha come corda quella  di un angolo pari alla latitudine della stella  ed è proprio di 13751 unità:

                                                               sen b = 13751/21600 = 0,63662…

con b = 39° 32,4’.

La circonferenza inoltre di 2,23,21,0 unità, cioè sessanta volte la longitudine iniziale di Sirio, ha come diametro, cioè due volte il raggio

                                        12 (13751) – 12,24 = 164268 unità

Il valore di p dato dal rapporto (2,23,21,0/164268) è straordinariamente approssimato, e ancor più se si sottrae un’unità alla misura del diametro. In notazione sessagesimale l’ultimo rapporto risulta

p         =  3,8,29,44,0,…

Si rilevi come Parmenide ponga il termine cerchio al verso 8 e il celebre verso sulla verità ben rotonda al verso 29 e la dea al verso 22 e il proemio consti di 32 versi.  E’ questo, ci pare, un’ulteriore indizio, se non si vuole ancora accettare come una prova, del sistema arcaico di comunicazione del sapere presente nel proemio e magistralmente impiegato anche da Dante nella sua opera. Tuttavia questo sistema è pur sempre nelle parole della dea “un ordinamento ingannevole dei miei versi” (Fr. 8, 52).

Il tempio maggiore sull’acropoli  presenta caratteristiche meritevoli di essere indagate. La misura dello stereobate del tempio maggiore, sull’acropoli, sono  m. 19,35 per  m. 32,50 (13) equivalente in modo significativamente approssimato all’area di un cerchio il cui raggio sia di m. 10 xÖ2.  Questa è una semplice curiosità che dipende dalla trasformazione dell’area di un rettangolo in quella di un cerchio, seguendo la suggestione della dea che invita ad apprendere prima di tutto il cuore immobile della verità ben rotonda. Invece si può cercare di capire perché la larghezza esprima in metri  lo spostamento annuale del nodo ascendente lunare. A questa domanda non siamo in grado di rispondere, non essendoci studi scientifici sulla teoria della costruzione del tempio antico. E’ questo un ambito di ricerca irto di insidie, aperto alla genialità dei dilettanti, ambito analogo a quello che stiamo esponendo sulla composizione letteraria del testo arcaico.

La sequenza degli eventi: l’evento iniziale, vv.1-3

Cavalle, quelle che mi portano fin dove giunge lo slancio dell'animo,

erano con me, dopo  che mi spinsero sulla molto famosa  via

della demone, che per ogni luogo abitato porta l'uomo che sa.

L’esordio repentino dei primi tre versi  si giustifica per quelle regole della composizione arcaica che stiamo cercando di individuare. Le cavalle che lo portano non sono quelle che, nell’ipotesi che il poema sia stato recitato la prima volta in occasione della costruzione del tempio maggiore sull’acropoli verso il 480-470 a.C.,  forse il pubblico ha visto arrivare, ma quelle cavalle che, secondo i racconti di quella cultura, trascinano il carro solare. Allora l’espressione “essere portato dalle cavalle del carro solare” più che contenere un simbolo, collegabile con il mito della rinascita e perciò rinviare ad un viaggio ultraterreno dell’anima, come si trova anche attestato in raffigurazioni tombali a Paestum di epoca posteriore, è una metafora e come tale deve essere intesa. Se il corso diurno e annuale del Sole è raffigurato dall’immagine del carro trascinato dalle cavalle, chi tale corso osserva, può dire di essere portato dalle cavalle, con le quali ha perciò una relazione di vicinanza e di accompagnamento. La diretta osservazione del Sole non è possibile se non al momento del sorgere,  fin quando la luce non divenga abbacinante, o poco prima del tramonto, cosicché nella proposizione relativa del v. 1 c’è il  riferimento alla difficoltà di una diretta osservazione del Sole, giacché le cavalle portano il pensatore fin dove lo sorregge lo slancio o la forza del suo animo. L’azione delle cavalle però  lo spinge proprio a rivolgere lo sguardo verso il Sole che sta culminando.

Il primo intervallo dunque da ricercare è quello che riguarda l’evento che spinge Parmenide sulla via della demone, evento indicato nel primi tre versi. In essi  i termini significativi di cui rintracciare le occorrenze sono  cavalle e via. Con le occorrenze del primo termine si  fornisce il tempo iniziale, mentre con le occorrenze di via (2,5,27) si deve trovare l’intervallo  a partire da quel tempo. Trattandosi di un evento espresso dall’azione violenta delle cavalle e queste sempre nel proemio sono legate al carro e sapendo che il tempo iniziale è relativo ad un plenilunio si dovrà dividere per 2 o il numero cinque o il numero ventisette. Non può essere il primo termine perché al v. cinque, collegate alla via, sono le fanciulle, che sono in relazione alla luna.

                      Per quella via mi slanciavo; per di là infatti  mi portavano le molto  palesanti  cavalle

5                che il carro trascinavano, mentre fanciulle  precedevano sulla via.

Dopo 13,5 (27/2) mesi dall’inizio, con il tempo segnato da 3,17,4 +13;30 mesi , avvenne qualcosa di violento concernente il Sole che indusse Parmenide nella sua ricerca a percorrere per primo una strada, lontana dal sentiero battuto dagli uomini, come recita il v. 27 e lo pose sulla via della demone. La demone è lo zenit del luogo, chiamato Citerea da Manilio, e la via il meridiano, l’arco verticale che congiunge il  Nord  al Sud. Non siamo ancora in grado di calcolare il valore di longitudine del Sole e quello del nodo lunare per questo novilunio per sapere sulla base del testo di Parmenide che si tratti proprio di un’eclisse solare, come per altra fonte, le tavole cioè dell’Oppolzer, siamo giunti  a sapere.

Le Fanciulle

Le fanciulle indicano la luna alle sue fasi e occorrono ai vv. 5,9,15,21. La sistematica osservazione del Sole e della luna sia sull’orizzonte che al meridiano dopo l’evento delle cavalle, permise a Parmenide di osservare alcune eclissi lunari.  Esse infatti abbandonano le case della notte  al v. 9. Al v. 5 occorre il termine Fanciulle, sicché la prima di queste eclissi lunari capitò a cinque mesi e mezzo dopo l’eclisse solare, a 19 mesi dall’inizio indicato dalla struttura a chiasmo delle occorrenze del termine cavalle.

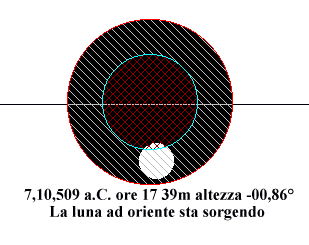
Fig. 8 .  Simulazione al computer  dell’eclisse con il programma
Eclipse v4.60 di Marco Menichelli

Si osservi come la luna sia ancora velata prima del suo sorgere e contemporaneamente stia tramontando il Sole. Per la parallasse essa è già visibile.

Nel precedente studio avevamo proposto di intendere il volteggiare dei battenti della porta eterea, della porta in cielo, come la descrizione della massima variazione del movimento in declinazione della Luna, in conseguenza della coincidenza del nodo ascendente lunare con il punto vernale. Ricordiamo che il punto vernale (Fig.1) è l’intersezione dell’eclittica sul piano dell’equatore celeste, che avviene quando il Sole passa dall’emisfero australe a quello boreale, da sud a nord.

Al v. 15 occorre il termine Fanciulle, quelle che persuadono Dike che molto punisce a sfilare i chiavistelli, di permettere cioè alla luna di superare i punti solstiziali segnati dall’altezza massima e minima del Sole al tempo dei due solstizi. Questi sono i chiavistelli. Ora quindici mesi dopo la prima eclisse lunare e 34 dall’inizio avviene questa coincidenza. La distanza della luna dal  nodo ascendente lunare è pari alla sua longitudine, sicché la longitudine del nodo ascendente lunare è 0° e tale plenilunio può essere assunto come  un inizio del ciclo dei nodi lunari di 18,6 anni.

Il sistema di calcolo delle longitudini al plenilunio dell’apertura della porta in cielo

Proviamo a calcolare la longitudine della luna dopo 34 mesi assumendo che il Sole si trovi inizialmente a 0°. E’ sufficiente calcolare l’incremento in longitudine del Sole per quell’intervallo. La formula in notazione simbolica è la seguente

                                                               l° (Sole) = l°(0) + Dl°

che significa che la posizione attuale del Sole sull’eclittica al novilunio o al plenilunio è data dalla somma della posizione iniziale con l’incremento in longitudine per il tempo trascorso dall’origine. Poiché l’incremento significa velocità per unità di tempo, possiamo vedere nel termine cavalle il passo che il Sole percorre nell’unità di tempo e nel termine carro la posizione del Sole sull’eclittica, cioè la sua longitudine.

                La procedura di calcolo è la seguente:

                Si moltiplica il numero dei mesi per il numero degli anni del ciclo e si prende il resto della divisione per il numero dei mesi del ciclo.

                                                                              34 x 521 = 17714

                                                                              17714 : 6444 = 4826 + 2x6444

                                                                              Resto = 4826

                Si moltiplica il resto per 30° e si divide per il  numero degli anni del ciclo

                                                                              4826 x 30° = 144780°

                                                                              144780° : 521 = 277,888°….

                Questo è l’incremento in longitudine del Sole sull’arco più lungo e più veloce. Si deve dunque ridurlo proporzionalmente al rapporto 521/557  valido sull’arco più breve e più lento.  Si ottiene  il valore di

                                                                              259,928°……

che supera il punto di discontinuità di 142° di ben  117,928°…. che a sua volta deve essere corretto in rapporto a 557/521,ottenendo 126,076°…

                Il Sole dopo 34 mesi dall’inizio con longitudine 0° si trova a gradi

                                                                              142° + 126,076°…=  268.076°…= 268°  4’

e la luna si trova a

                                                                              88° 4’ con distanza dal nodo ascendente lunare di 88° 4’

e la loro differenza è 0°. In questo plenilunio avvenne la coincidenza del nodo ascendente lunare con il punto vernale, in altri termini, la longitudine del nodo ascendente è 0°. Applicando le formule di Meeus si hanno i seguenti dati:

Per il plenilunio del  24 dicembre del 508 a.C.

                                               La luna si trova a                               88° 13’

                                               Distante dal nodo                                                88° 2,4’

                Il dato calcolato secondo questa lettura del proemio e secondo gli algoritmi della cosmologia arcaica è così straordinariamente prossimo ai calcoli attuali , che si stenta ad accettare un tale risultato. 

Poiché il ciclo dei nodi lunari è lungo 18,6 anni, pari approssimativamente a 230 mesi lunari , lo spostamento retrogrado del nodo ascendente lunare per ogni lunazione è

-360°/230 m  =  - 1,5652°.... ogni mese lunare

L’azione delle cavalle del v. 2 avvenne 20,5 mesi prima sicché la longitudine del nodo ascendente lunare si trova ad essere

                                                               -20.5 x –1,5319°… =  32°  5’

e con la medesima procedura di prima si può calcolare la longitudine  della congiunzione di Sole e Luna. Essa è di  31° 45’ e la distanza dal nodo (31° 45’ –32° 5’) di ben 359° 20’. Poiché questo valore rientra nella zona dei nodi ed è vicinissimo a 0°,  si  è  in condizione di un’eclisse solare  trovandosi la luna ben prossima al piano dell’eclittica. Dalla lettura del testo, sia pure guidata dalla notizia extra-proemio dell’eclisse solare, si deduce che  l’evento violento, dato dal verbo spingere del v. 2 è un’eclisse solare vista e osservata da Parmenide.

 I valori calcolati secondo gli algoritmi di Meeus  sono i seguenti:

                                               La longitudine del Sole e della Luna    31° 34,8’

                                               La distanza dal nodo ascendente             359° 25,8’

con una sorprendente vicinanza ai valori  trovati  secondo questa lettura del proemio.

L’eclisse lunare. Le Eliadi vv. 6-10 e vv. 20-21

Non abbiamo ancora trovato il tempo per l’eclisse lunare con quelle caratteristiche descritte nei vv. 8-10:

                quando si affrettavano a accompagnare le Fanciulle solari, avendo abbandonato le case della notte, in direzione della luce, verso l’oriente, essendosi strappate i veli dal capo.

La Luna ritorna alla piena visibilità prima di tramontare oppure esce solo dall’ombra ,rimanendo nella penombra, anche quando è sotto l’orizzonte.  Le kourai solari, le figlie del Sole, si trovano al v. 9: 9 mesi dopo il plenilunio della coincidenza del nodo ascendente lunare con il punto vernale dei vv. 15-20, e 24 mesi dopo la prima eclisse lunare e 43 mesi dal tempo dato come inizio è avvenuta un’eclisse lunare.

                Su quale tratto dell’eclittica si trova la Luna? Sul tratto più veloce o su quello più lento? Il testo  parla di un affrettarsi, sicché la Luna trovandosi  in opposizione al Sole, essa dovrebbe essere dopo il grado 342 e il Sole dopo il grado 142.

                Si calcoli la longitudine della Luna dopo 43 mesi assumendo che il Sole si trovi all’inizio a 0°

                Si moltiplica

                                                                              43 x 521 = 22403

                Si divide per 6444

                                                                               22403 : 6444 = 3071 + 3 x 6444

                Si prende il resto 3071

                                                                              3071 x 30° =  92130°

                Si divide per 521

                                                                              92130° : 521 = 176,83°…

                Si corregge il dato per l’arco lento trovandosi il Sole su quell’arco di eclittica

                Si moltiplica per 521 e si divide per 557

                                                                              92130° : 557 = 165,40°…

                Si è ottenuto l’incremento di longitudine del Sole, il passo compiuto dalla cavalle per 43 mesi  iniziando la corsa da un punto che si trova sull’arco lento. Il carro del Sole si trova  a

                                                                                  165° 24’

                E’ stato superato il punto di discontinuità della velocità solare e qui Eraclito avrebbe detto che  Helios invero non oltrepasserà le misure: in caso contrario lo scoveranno le Erinni, ministre di Dike. (DK A 81, trad. G.Colli). Si deve pertanto correggere , con un termine di sapore anassimandreo,  quanto è stato superato.

                                                               165° 24’ – 142° = 23° 24’

                                                               (23° 24’) x557/521 = 25° 01’

Il Sole si trova sull’arco veloce a

                                                               142° + 25° 01’ = 167° 01’

e la Luna si trova a 180° dal Sole a

                                                               167° 01’ + 180° = 347° 01’

e il v. 9  riferisce  precisamente che le eliadi si affrettavano, trovandosi la Luna in opposizione al Sole che  sta percorrendo l’arco di eclittica più lungo e più veloce.

Si può inoltre calcolare la longitudine del nodo lunare, ricordando che l’opposizione è avvenuta 9 mesi dopo la coincidenza della longitudine lunare con  il valore di distanza dal nodo. Essa è

                                                               360° - 9 x (360°/230) = 345° 54’

la Luna si trova molto prossima al piano dell’eclittica e può essere eclissata dall’ombra della terra.                     

                L’eclisse individuata pare perfettamente conforme ai versi 6-8 di Parmenide, in quanto le Fanciulle si affrettano nel passaggio del Sole dall’arco lento a quello veloce, e l’asse dei mozzi emette il suono di siringa (v.6)  in

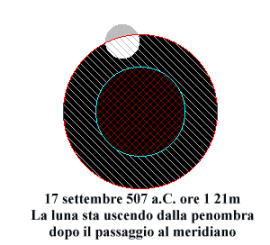
Fig. 9 .  Simulazione al computer  dell’eclisse con il programma
Eclipse v4.60 di Marco Menichelli

quanto il rapporto tra i due archi è pari a quello di un intervallo musicale (5/4), come avevamo proposto di leggere questa metafora parmenidea  riferita alle due velocità solari. La interpretazione di questa metafora aprì la strada alla ricerca della struttura tecnica della cosmologia arcaica. L’errore dello studio precedente fu invece quello di aver ipotizzato un’eclisse solare, che ci fu al novilunio precedente, e non un’eclisse lunare e di aver  tradotto l’avverbio di tempo quando con ogni qual volta. 

La Luna è uscita dalla penombra quando già aveva oltrepassato il meridiano,  in direzione dunque dell’oriente, perché dall’oriente sorge la luce.  L’altezza massima della Luna fu di 44,81° quando cominciava ad uscire dall’ombra ed entrare nella penombra  proprio là dove ci sono le porte dei cammini della notte e del giorno, v.11. Queste porte non sono solo semplicemente l’oriente e l’occidente, ma sono anche sul meridiano segnate dall’altezza massima e minima del Sole ai due solstizi. La Luna avendo una variazione in declinazione superiore a quella del Sole si trova a volte ad oltrepassare i due punti  del meridiano e precisamente durante il mese sidereo, quando è avvenuta la coincidenza del suo nodo con il punto vernale.  Le porte nell’etere del v. 13 sono da vedersi sul meridiano e sono fornite di  grandi battenti, (v.10).  Questi battenti volteggiano quando Dike sfila i chiavistelli, i punti solstiziali sul coluro dei sostizi, sicché l’oscillazione del piano della Luna  sulla sfera celeste deve essere vista al meridiano e produce quell’atipica apertura della porta costruita nell’etere.

                Parmenide fornisce dunque il tempo di un plenilunio e il tempo, 34 mesi lunari dopo, in cui la longitudine della Luna è identica al valore di distanza del nodo ascendente lunare e fornisce il ciclo in base al quale calcolare secondo gli algoritmi arcaici la longitudine del Sole e della Luna. Tale ciclo è dato dalla differenza in longitudine tra le due stelle della costellazione dell’Auriga.

                Dike, la Giustizia che molto punisce

                La giustizia cioè Dike occorre sia al verso 14 che al verso 28. Nello studio precedente avevamo identificato la Giustizia che molto punisce nel coluro dei solstizi (Fig.1), mentre la Dike senza aggettivi nel meridiano di origine passante per i punti equinoziali. Si può  invece pensare che il nome per il meridiano d’origine sia Themis del v.28. Questo significato riguarda il piano cosmografico.  I due termini numerici sono in progressione geometrica e occorrendo la prima volta Dike in un contesto riguardante la rivoluzione dei nodi  viene data la seguente legge di calcolo del tempo che si trova espressa nella tetraktys pitagorica:

                Nel tempo in cui il polo celeste compie un arco di 14° 28’ vi sono ben 56 rivoluzioni dei nodi.

Non crediamo che vi sia anche un riferimeto al valore della differenza tra l’anno sidereo e quello tropico per il medesimo intervallo, anche se questa grandezza (14;42 giorni) è legata al sistema arcaico di equivalenze.  Invece pensiamo che venga data la seguente informazione: trovandosi Parmenide nella casa della dea (Sirio) ed essendovi giunto con il carro e le cavalle e con l’indicazione delle Fanciulle del v. 21, viene suggerito che la longitudine della Luna è  prossima a quella di Sirio. Il tempo trascorso dall’origine in Gemelli è di

                                                                                              14,42,0 mesi 

corrispondente al tempo trascorso dall’inizio arcaico greco a

                                                                                              3,17,25 mesi

21 mesi dunque dal tempo indicato dalla struttura a chiasmo, che corrisponde al 5 dicembre del 509 a.C.

Con la medesima procedura di calcolo si trova che per un intervallo di 21 mesi l’incremento in longitudine del Sole, metaforicamente le cavalle portano Parmenide alla casa della dea, situa la  Luna a  69° 7’ 56”. La longitudine di Sirio espressa in mesi è 17,5,21. Si trasformino i mesi in anni tropici e si divida per 72 e si ottiene la longitudine di Sirio in  69° 5’ 5”.

Con questa informazione risulta completo il sistema che Parmenide  comunica con i suoi versi, fornendo la longitudine del  Sole e della Luna ad un plenilunio, quello avvenuto 21 mesi dal tempo indicato inizialmente con il sistema delle differenze successive delle occorrenze del termine cavalle.

L’eclisse lunare precedentemente trovata , quella del 17 settembre 507 a.C., tuttavia, è avvenuta dopo l’evento descritto nei vv. 15-20, sicché non può essere quella indicata dai precedenti versi.6-8, ma tutt’al più una indicata in modo generico ai versi. 20-21,

qui dunque per le medesime (porte)

le fanciulle direttamente guidavano lungo la via carraia carro e  cavalle  .

Questi versi paiono infatti esprimere la conclusione di un percorso di conoscenza , in seguito al quale Parmenide è in grado di calcolare le condizioni di eclisse al plenilunio., avendo egli individuato due pleniluni: quello in cui la luna ha longitudine pari a quella di Sirio e quello dell’apertura della porta. La luna ha infatti attraversato l’eclittica al punto vernale quasi sette giorni prima , sicché le fanciulle del v. 15 indicano la luna al primo quarto, quelle che con soavi discorsi  (rapporti) persuadono Dike.  Infatti con un progresso giornaliero della Luna di circa 13°  sull’eclittica, si trova, , per  il tempo della coincidenza del nodo lunare con il punto vernale, 6.7 giorni circa prima del plenilunio, cioè la Luna al primo quarto. I dati iniziali  per il calcolo sono dunque, per il nodo ascendente lunare, il plenilunio del 24 dicembre del 508 a.C. e, per la longitudine della Luna, il plenilunio del 5 dicembre del 509 a.C.

Per l’eclisse dei vv. 6-10 si trova un plenilunio, anteriore al  24 dicembre del 508 a.C., durante il quale la Luna appare velata mentre sta tramontando, sta abbandonando le case della notte del verso 9. La simulazione con il programma al computer lo mostra chiaramente.

Fig. 10 .  Simulazione al computer  dell’eclisse con il programma
Eclipse v4.60 di Marco Menichelli

 

Il tempo di questo plenilunio espresso secondo il sistema arcaico è 3,17,35 mesi dall’origine greca, e 14,42,10 mesi dall’origine posta in Gemelli. Al verso 10 c’è il riferimento alle Eliadi che si strappano il veli dal capo , al tramonto o subito dopo il tramonto.  Tre mesi dopo le Eliadi persuadono Dike a sfilare i chiavistelli della porta.

 

 

 

 

 

 

La sinossi degli eventi

 

Dato il tempo fornito dalla struttura a chiasmo delle cavalle , cioè 3,17,4 mesi dall’origine greca, il quadro sinottico sugli eventi narrati è il seguente:

 

 

 

 

La longitudine di Sirio è 17,5,0 mesi

La distanza di b Aur da Capella è 7° 14’ 10” pari a 521 anni e 6444 mesi

                                    La longitudine di b Aur è  13,27,14 mesi

                                   

1) 27/2 mesi dopo; vv.2,5,27 via

                                    L’evento dell’eclisse solare dei vv. 1-3

                                    al tempo dato da  3,17,17;30

 

2)            5.5 mesi dopo l’eclisse solare; v.5  Fanciulle

                                    la Luna sorge velata  al tempo dato da  3,17,23

 

3)                 12 mesi dopo, al tempo indicato da 14,42,10 mesi

e 3,17,35 dall’origine greca

la Luna tramonta velata vv.6-9 v.9 Fanciulle

                       

4)            3 mesi dopo

al tempo dato da 14,42,13 mesi = T greco + 3,17,38

e 15 mesi dalla prima eclisse lunare

la longitudine del nodo ascendente lunare è 0° ; v. 15 Fanciulle

                       

5)            9 mesi dopo, al tempo dato da 14,42,22 mesi = T greco + 3,17,47 mesi

La luna esce dall’ombra dopo il passaggio al meridiano

vv. 20-21 v. 21 Fanciulle

           

                        6)            22 mesi prima, cioè a 3,17,25 m.; v. 25 casa

al tempo dall’origine in Gemelli di 14,42,0 mesi ; vv. 14,28  Dike

                                    la longitudine della Luna coincide con la longitudine di Sirio; vv. 24-25

                       

7)            e mezzo mese dopo al tempo dato da 3,17,25;30

                                    la longitudine di Eros è 25-17, 25+17-3,0 mesi = 8,39,0 mesi

                                    Eros era apparso durante la prima eclisse solare e si trova al Fr.13

 

 

 

 

 

 

 

Per una migliore comprensione della struttura del proemio e degli eventi narrati in esso, il precedente quadro sinottico può essere rappresentato mediante la seguente tabella:

 

 

Gli eventi e la struttura del Proemio
Principio	Tempo greco	Tempo di Parmenide
11,24,35 mesi	3,17,4 mesi	Dea: 17,5,0 m	Dl: 7° 14’ 10”	b Au: 13,27,14	Tempo iniziale -509,3,27
Porte:11,13	Caval.,1,4,21,25	Dea,22	Aurighe: 24		vv. 1-24
	Via,2,5,27
	+27/2 m
	3,17,17:30 m	Eclisse solare al meridiano			vv. 1-3: via della demone	- 508,4,28
	+ 5.5 m				v. 5 fanciulle
	3,17,23 m	Eclisse lunare al sorgere			vv. 4-5	-508,10,7
	+12 m
	3,17,35 m	Eclisse lunare al tramonto			vv. 6-10  v.9, fanciulle solari	- 507,9,27
	+ 3 m
	3,17,38 m
			L° nodo = 0°	Primo quarto	v. 15: fanciulle	- 507,12,17
		Apertura porta	Plenilunio		vv.15-20	- 507,12,24
	+ 9 m
	3,17,47 m	Eclisse lunare al meridiano			vv. 20-21 v.21 fanciulle	-506,9,17
	- 22 m	Saluto della dea			vv. 22-28
	3,17,25 m				v. 25 nostra casa
Dike 14,28 m
14,42,0 m		Parmenide giunge nella casa della dea			Dea: 17,5,21	-508,12,5
		La L° della Luna  in Gemelli coincide con la L° di Sirio
	Carro 5,21
	- 5,-21 m ?
	3,12,4 m
14,36,39 m		Nascita di Parmenide ?			Dea , 17,0,0	-534,12,23

 

 

            L’arco di tempo degli eventi descritti nel proemio comprende 29,5 mesi, dal 28 aprile del 509 a.C. al 17 settembre del 507 a.C. Le osservazioni comportano un’età  non più giovanissima e si oppongono alle ipotesi di porre la nascita di Parmenide  intorno al 510 a.C. per  accordarle alle notizie che Platone ci dà nei suoi Dialoghi.  La nostra lettura è in accordo con quanto Diogene Laerzio riporta, seguendo la cronologia di Apollodoro, secondo la quale  Parmenide “fiorì nella sessantanovesima Olimpiade” (504-501 a.C.) (Diogene Laerzio, Vite dei filosofi, IX 23). Una problematica indicazione dell’età di Parmenide si può forse ravvisare nella  “moira  non avversa” del  v. 26, che insieme a Dike e Themis portano il pensatore alla casa della dea, come mostreremo  in un successivo paragrafo.

 

 

Poiché 21 mesi dopo il tempo iniziale v’è la coincidenza della longitudine della Luna, che si trova in Gemelli presso d Gem, con la longitudine di Sirio, a questo punto è possibile calcolare la longitudine iniziale del Sole  che risulta essere al plenilunio di primavera del 510 a.C. di 359° 57’ ; quella della Luna alla coincidenza del nodo ascendente lunare con il punto vernale è di 88° 1,74’, la longitudine del Sole al novilunio dell’eclisse è di 31° 42’ e la distanza dal nodo  ascendente lunare  (31° 42’ – 32° 5’)  risulta di 359°  23’ con un ulteriore avvicinamento ai calcoli secondo le procedure attuali. La longitudine di a Tauri trasformata in gradi è  circa di 34° 58’,  e risulta essere la stella, o meglio, il decano più vicino al Sole e al meridiano, la stella più vicina alla Demone che tutto governa del fr.12 e del fr. 13, come si può vedere nella mappa ricostruita dal programma al computer (Fig.11).

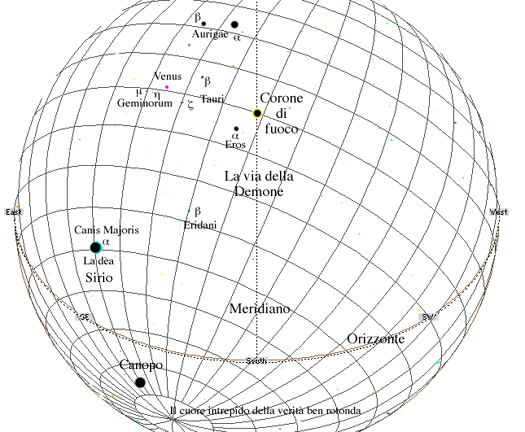
Fig. 11  Mappa del cielo sopra Velia
elaborata al computer con Voyager II (Carina Software)

 

Per la ricerca del catalogo stellare e i diversi tempi di origine.

 

                La conoscenza della longitudine di Eros è fondamentale per la cultura arcaica greca e non solo greca, perché si può calcolare quando la stella segnò l’equinozio di primavera. Facendo i calcoli secondo questo sistema, Eros-Cupido, l’occhio del Toro, segna l’equinozio, ha cioè longitudine 0° quando sono trascorsi ben 21780.5 mesi dall’origine in Gemelli. Per Esiodo è il primo nato e ciò significa che la lettura della Teogonia presuppone che il suo racconto narri come erano a quel tempo gli dei e come sia possibile calcolare il tempo delle azioni gloriose degli uomini, cantate dai poeti.

Questa conoscenza è d’altronde strategica per aggiungere altre stelle al catalogo stellare, che stiamo rinvenendo nel proemio di Parmenide secondo il codice di memorizzazione arcaica. Le stelle non sono menzionate nei frammenti pervenutoci, ma esse sono importanti se solo andiamo in Oriente e sono stelle legate alla dea.

                                Quando a Tauri misura la longitudine corrispondente a 13751 mesi lunari, longitudine iniziale di a Geminorum, Castore  misura come sua longitudine la longitudine di Regolo (a Leonis) al tempo zero.

 

 

                                Per  DT = 21780.5 + 13751 mesi

a Tauri = 13751 mesi,

a Geminorum = 13751 + 21780.5 + 13751 mesi = 49282.5 m

a Leonis = 49282.5 + 21780.5 + 13751 mesi = 84814 mesi.

 

                Inoltre, se si somma la longitudine iniziale di Sirio con quella iniziale di Regolo, si ottiene un numero di mesi lunari pari a 57883.5 equivalenti a 65° di precessione e a 4680 anni. A questo punto la dea di Parmenide appare in compagnia del leone e brandisce un arco come l’Isthar assira o l’Inanna sumerica, il cui tempio si trova in Uruk, secondo la saga di Gilgames.

L’arco di Isthar è il ciclo lunisolare che collega 4680 anni tropici a 57883.5, sulla cui base è possibile dopo aver trovato i parametri del sistema arcaico, i due archi in cui viene suddivisa l’eclittica e le due velocità , è possibile cioè calcolare le longitudini del Sole per qualsiasi numero di mesi si voglia. Il leone è raffigurato assieme ad Isthar (Fig.14) nelle culture medio-orientali.

L’arco di eclittica che collega a Leonis a z Tauri, una stella legata all’Auriga nella cultura elamita, è ancora di 65°. Ciò significa che viene assunto nella tradizione arcaica che al tempo d’origine z Tauri sia per la sua longitudine il punto simmetrico a Sirio.

Infine nei documenti  antichi viene assunto che sono necessari 4680 anni dall’origine in Gemelli affinché a Piscium segni l’equinozio di primavera. Ma questa informazione si ritrova più facilmente nei documenti della tradizione cristiana che nei documenti della cultura arcaica, anche se numerose sono le rappresentazioni dei Pesci nella pittura vascolare Etrusca e in quella di Argo. 

Anche Eros ha il suo arco nella raffigurazione vascolare e nei  testi letterari. Il suo arco è dato dal  ciclo che collega 21780.5 mesi a 1761 anni solari tropici, con questa particolarità che è sufficiente conoscere il ciclo di Eros per sapere quando a Tauri segnò l’equinozio di primavera.

Moira, Themis e Dike

Nelle parole di saluto della dea c’è però qualcosa che si riferisce direttamente a Parmenide.

salve! poiché non una Moira avversa ti ha mandato a percorrere per primo

questa via, - essa è infatti lontana da quella battuta dagli uomini -

ma Themis e Dike.
Fr. 1,26-28.

I termini impiegati non significano semplicemente che  il giovane Parmenide è sotto una buona sorte. Themis e Dike hanno una relazione con la giustizia, la prima regola i rapporti  tra i sessi nell’ambito della famiglia e la seconda i rapporti tra i cittadini nell’ambito della polis.  La città fiorisce aumentando la ricchezza dei suoi cittadini se è sotto il governo di Dike . Un passo di Giamblico attribuisce alle leggi nella città la medesima funzione che hanno  Themis e Dike  in cielo, essendo le prime espressione delle leggi che sono nel cielo. (De Vita Pithagorica, 26, edidid L.Teubner). Themis si troverebbe presso Zeus,  Dike presso Pluto.  Questo per quanto riguarda il senso generico dell’affermazione. Tuttavia moira ha un significato tecnico  in astronomia, designando il grado della divisione del cerchio. Pertanto un grado non avverso può alludere ad una circostanza concernente la nascita. Senza invocare un riferimento a pratiche astrologiche o ad oroscopi, è necessario riferire il frammento sul  congiungimento dei sessi e sul doloroso parto, che sono infatti sotto il governo della demone che tutto governa, come recita il Fr. 12:

 

                                                Dovunque, infatti, essa presiede al doloroso parto e alla congiunzione,

                                                Spingendo la femmina ad unirsi col maschio, e, all’inverso, di nuovo,

                                                Il maschio con la femmina. (trad. G. Reale)

 

e come Manilio afferma dopo i versi citati sulla sede in cielo di Citerea:

 

                                                               et velut in facie mundi sua collocat ora,

                                                               per quae humana regit. Propria est haec reddita parti

                                                               uis, ut conubia et thalamus taedasque qubernet:

                                                               haec tutela decet Venerem, sua tela movere.

                                                               (Astronomicon, II,923-926)

 

 

e nella traduzione di Massimo Candellero : Alla sommità del cielo, là ove gli astri cessano di salire ed iniziano invece a declinare, là ov’essi ad eguale distanza si trovano dal loro sorgere come dal loro tramontare, in quella regione che pare tenere sospeso l’intero mondo in un perfetto equilibrio, là la dea Citerea ha fissato la propria sede, in maniera così da mostrare all’universo intero le sue grazie, con le quali essa governa le cose umane. Funzione tipica di questa regione è quella di presiedere alle unioni, al talamo nuziale, agli sposalizi: tutti compiti degni di Venere e dei dardi che essa suole scagliare. (14).

Nel frammento parmenideo non si ritrova tutto il sapore astrologico del poeta latino, che poco più avanti ricorda ancora il nome di Fortuna per la sede della Demone,  ma con brevissimi cenni la sostanza della dottrina tradizionale.

                C’è dunque da domandarsi se Parmenide non abbia inteso comunicare per mezzo delle  parole della dea  un invito a ricercare il tempo della sua nascita, un tempo espresso da una  moira non avversa. Tra i termini numerici delle occorrenze  vi sono quelli relativi al carro, che insieme a cavalle e fanciulle occorre al verso 5 e 21. Questi due termini numerici  non hanno avuto alcuna funzione per determinare gli eventi finora descritti.

                Ora, nella situazione prevista dal proemio, siamo al plenilunio in cui la longitudine della Luna in Gemelli coincide con quella di Sirio, sicché Parmenide è giunto alla casa della dea sul carro trainato dalle cavalle con le Eliadi che indicavano la strada. La longitudine di Sirio per quel plenilunio si esprime in mesi  17,5,21. Non ci vuole molto a scoprire che in questa espressione sono presenti proprio i termini numerici  dei versi in cui occorre il termine carro.  Si può forse congetturare che quando Sirio alias la dea misurava 17,0,0 mesi, cioè 5,21 mesi prima, Parmenide nasceva? Quale valore può avere la congettura che pone l’età di Parmenide al 5 dicembre del 509 a.C. quasi di 26 anni , essendo egli nato, secondo questa lettura, al plenilunio del 23 dicembre del 535 a.C.?  Si osservi come il termine Moira si trova proprio al verso 26 del proemio e in base alle regole di composizione e a come è stato letto il proemio,  sembra non essere una semplice congettura.

La nascita di Parmenide non è  un evento celeste, controllabile mediante calcolo, ma solo con la fonte storica di Apollodoro che pone l’acme del pensatore alla sessantanovesima Olimpiade (504/501), in sufficiente accordo con quanto da noi proposto. Tuttavia questa lettura ci lascia perplessi , perché  non c’è alcun rapporto intrinseco  tra l’evento della nascita  e il contenuto astronomico del proemio.

Poiché nei vv. 26-28 è messo in rapporto Moira  con  Themis e Dike e la prima come nome comune significa tecnicamente grado, possiamo vedere nell’angolo di 26° l’altezza approssimativa del sole al solstizio invernale alla latitudine di Velia (40° 8,831’), cioè qualcosa che è  precisamente descritto e narrato in riferimento alle porte dei cammini della notte e del giorno e all’apertura volteggiante dei battenti, attraverso le quali deve passare Parmenide  sul carro per giungere alla casa della dea e nei termini numerici delle occorrenze del termine ‘carro’ (5,21) l’altezza massima  della Luna al passaggio al meridiano, quando la sua declinazione sud è massima oppure la differenza tra le due declinazioni del Sole e della Luna., cioè 5° (21+5)’. Con questi dati si trova che l’altezza h della Luna quando ha la massima declinazione sud  sia, alla latitudine di Velia

 

                                                               h_min = 26° -5° - 26’ = 20° 34’

Se si avesse il valore d di declinazione sud della Luna si avrebbe la possibilità di ricavare la declinazione massima del sole al solstizio invernale e di trovare la misurazione effettuata della latitudine a Velia.  Per la ricerca di questo dato, che è in rapporto alle funzioni del cerchio, i versi possono essere i seguenti:

 

v. 29 ………. verità ben rotonda

v. 8 cerchi ………

 

I possibili valori di declinazione

                                                               d_max =  -29°  8’

oppure

                                                               d_max = - 29° (29-8)’

 

Con i precedenti dati di altezza del Sole e di differenza delle due declinazioni del Sole e della Luna , il valore di  d_max = - 29° 21’ è quello  matematicamente conforme e permette di trovare il valore dell’inclinazione del piano dell’eclittica sull’equatore celeste in 23° 55’ , vicino alla valutazione standard di 24° , e la latitudine di Velia in 40° 05’, una misura molto precisa.

 

Fig. 12 Rappresentazione delle altezze del Sole e della Luna
alla massima declinazione sud, nel giorno del solstizio invernale,
quando il coluro dei solstizi coincide con il meridiano.
I dati che sono stati letti e calcolati sono consistenti. Si può infatti calcolare l’angolo di amplitudine ortiva della Luna quando la sua declinazione misura – 29° 21’. Applicando la formula che esprime l’angolo in funzione della declinazione e della latitudine del luogo

sen Am= sen d/cos f

e si trova che Am = 39° 50,28’ un angolo molto prossimo a quello di 39° 58’ (Fig. 5), che l’asse del tempio maggiore sull’acropoli a Velia forma con la direzione nord-sud. Questa è una prova che il tempio costruito verso il 480 a.C. dipende direttamente dall’attività di osservazione astronomica e di elaborazione teorica di un nuovo modello da parte di Parmenide, descritta nel proemio, esattamente come se fosse un protocollo scientifico di ricerca. Ciò che vengono rappresentate nella Fig. 12 sono le porte dei cammini della notte e del dì e l’ampia apertura del verso 18. Questa apertura è costituita dall’arco di meridiano segnato dalla variazione di declinazione (da  d = + 29° 21’ a d = – 29° 21’ ) e quindi di altezza della Luna , da h =20° 34’ a h = 79° 16’. Queste porte non sono l’oriente e l’occidente, come invece la lettura di Porfirio propone, che però gli studiosi non hanno generalmente accolto, ma definite e segnate sul meridiano,

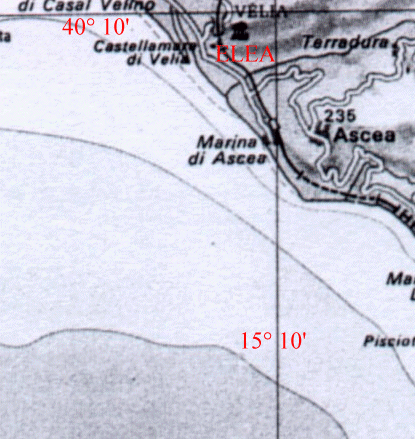
Fig. 13 Carta geografica per Velia
proprio sulla via della demone. Poiché è la Demone e non la Dea che presiede alla nascita e alla morte, non deve essere accettata pertanto la suggestione che vedeva nel complesso Moira Themis e Dike un possibile riferimento al tempo della nascita dell’Eleate.La rappresentazione cosmografica di Fig.12 è il contributo specifico di Parmenide alla storia dell’astronomia e comporta la comprensione del passaggio dal sistema locale dell’orizzonte a quello universale dell’eclittica e a quello dell’equatore celeste; comporta una elaborazione di strumenti matematici per trattare la corrispondenza delle altezze degli astri alla loro culminazione ai valori di declinazione sulla sfera celeste. Dai vv. 1-21 sono descritti eventi secondo la scienza arcaica; dai vv. 22-32 strutture cosmografiche coi i corrispondenti valori per la latitudine di Velia.

Può essere interessante per la comprensione delle parole della Dea osservare la situazione uranografica del cielo sopra Velia alla culminazione di Sirio nel plenilunio (- 508,12,5) in cui la longitudine della Luna coincide con la longitudine della stella, come si può vedere nella seguente simulazione al computer con Voyager I (Carina Software) e quella relativa alla culminazione della Luna  al plenilunio (-507,12,24) dell’ apertura della porta in conseguenza della coincidenza del nodo ascendente lunare con il punto vernale. E’ possibile vedere che le stelle dell’Auriga culminano vicinissime allo zenith.

 

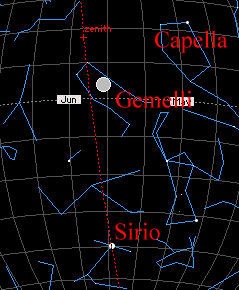
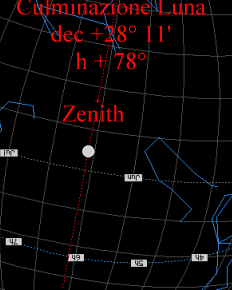
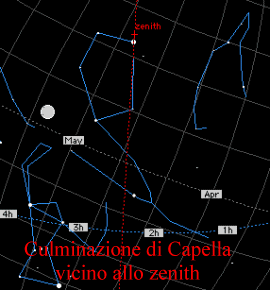
Ciò che nel proemio Parmenide descrive non è solo un viaggio di conoscenza, come abbiamo visto, ma anche

Fig. 14. Palazzo di Mari sec. XVIII a.C,
Investitura del re Zimri-Lim. da A. Parrot, Sumeri, pag. 279

 

una specie di investitura simbolica da parte della dea della verità ben rotonda.

Se ci trasportiamo in un’altra cultura, a Mari, 1200 anni prima, possiamo vedere un’altra dea molto simile a quella di Parmenide. Gli scavi archeologici di A. Parrot (15) hanno portato alla luce, nel palazzo di Mari del XVIII sec. a.C., un affresco (Fig.14) nella sala delle udienze in cui è rappresentata l’investitura del re di Mari da parte di Isthar. Essa stringe in mano un cerchio con  un cubito, simboli del potere dei re in quelle culture, eredi  di quella civiltà di grandi costruttori che furono i Sumeri. La loro  dea Inanna, lo splendore del cielo,  è la prima di queste grandi dèe  che dall’Oriente si manifestarono nelle culture del Mediterraneo.  I Focei provenendo dall’Asia minore portarono in occidente le loro tradizioni, che si ritrovano forse nel proemio di chi fu anche un legislatore e politico della città. L’immagine della dea dell’affresco che trasmette al re di Mari il cerchio e il cubito, simboli di conoscenza e di potere, è quella che più s’avvicina a quell’investitura nell’ordine del sapere e del potere implicita nelle parole della dea del proemio di Parmenide.

Egli ebbe modo pertanto di raccogliere l’eredità della Ionia, di quella scuola di Anassimandro, che per primo descrisse in una mappa la terra, con l’impiego di qualche sistema di proiezione. Nella Magna Grecia l’Eleate trovò il pitagorismo e quel sistema della Decade, la cui tradizione viene fatta risalire a Filolao e Archita e secondo una testimonianza di Lidus,  non tenuta in conto, anche a Parmenide.

                Sulla base di queste due osservazioni, si può già affermare che Parmenide rappresenta la sintesi scientifica dei metodi aritmetici dei Pitagorici e dei metodi geometrici della scuola ionica di Talete e precisamente dei metodi proiettivi di Anassimandro che disegnò una carta geografica dell’ecumene, della terra abitata.

Parmenide, secondo questa nostra intuizione, avrebbe rappresentato su di un piano la sfera celeste con i suoi cerchi, denominando anche tale rappresentazione to eon .Secondo una testimonianza di Eudemo di Rodi, lo storico della geometria, Parmenide avrebbe chiamato to eon la sfera celeste. Ricordando la critica a Parmenide di Aristotele, si può capirne la ragione quando chiama il pensatore e quelli della sua scuola gli stabilizzatori della natura. C’è tutta una tradizione dossografica che fa dell’Eleate un discepolo di Anassimandro e un’altra che lo collega direttamente ad Aminia pitagorico.

 

 

Il sistema di Parmenide: Le funzioni del cerchio e la rappresentazione della sfera celeste

 

                Il sistema arcaico presente nel proemio è quello condiviso dagli interlocutori di Parmenide, ma non crediamo sia quello che egli propone in alternativa alle opinioni dei mortali: non è quello che nasce dal cuore intrepido della verità ben rotonda del v. 29 che non è una semplice metafora ma la designazione sia del rapporto costante della circonferenza al diametro, sia del polo sud dell’eclittica come punto di origine della proiezione sul piano dell’eclittica come piano di proiezione della sfera celeste. Questa crediamo sia l’innovazione di Parmenide. A termine di questa esposizione possiamo accennare ad alcune ragioni che permettono di corroborare la nostra ipotesi di lettura.

                Per quanto riguarda il rapporto della circonferenza al diametro , la circonferenza è di  2,23,21,0 unità,  cioè sessanta volte la longitudine di Sirio al tempo zero, e il diametro di 45,37,47 unità. Nella espressione sessagesimale del loro rapporto

                                                                              p = 3;8,29,44,0,…

 

si  trova una corrispondenza dell’occorrenza di ‘cerchio’ al verso 8 e di ‘verità ben rotonda’ al verso 29 e di dea al verso 22, la metà del quarto termine e dall’esplicito numero delle ruote del carro al verso 7.

L’attività di osservazione del Sole e della Luna al meridiano comporta la misurazione di angoli delle altezze degli astri, presenti, come abbiamo visto, nel progetto costruttivo e del tempio e della Porta Rosa. Pertanto Parmenide fu portato a iniziare lo studio delle funzioni del cerchio, se voleva trattare in modo rigoroso il problema delle altezze degli astri alla loro culminazione e ha cercato una rappresentazione piana della sfera celeste. A sostegno della nostra lettura, oltre a quanto abbiamo mostrato con la Fig.12, c’è una testimonianza di  Simplicio su Melisso: Melisso parla di grandezza e non di estensione: (..) Egli chiama grandezza la sublimità dell’ipostasi ( 16). Se la prima affermazione della traduzione è comprensibile, tuttavia il sèguito non ha alcun senso, anche se nella poetica il termine greco definisce lo stile elevato o sublime. L’osservazione di Simplicio è preziosa perché indica che Melisso, seguace della scuola di Elea, considera gli angoli come grandezze, diverse appunto da quelle lineari, di superficie e di volume. Quegli angoli misurano l’altezza sull’orizzonte di un qualsiasi corpo. In astronomia e in navigazione si misura l’altezza di una stella alla culminazione e innanzi tutto l’altezza del polo per  determinare la latitudine del luogo. Il termine tecnico greco corrisponde al latino elevatio ,  e, per  dire l’elevatio poli, come espressamente afferma il Petavio nella sua opera non più letta dal titolo De doctrina temporoum (1627). Il passo di Simplicio va dunque tradotto: Egli chiama grandezza la culminazione del corpo preso ad oggetto di osservazione.

 Si può discutere se il cuore intrepido sia il polo sud dell’eclittica oppure il polo sud celeste. In questo ultimo caso si  anticipa  a Parmenide la costruzione di un astrolabio sia pur semplificato ma pur sempre un astrolabio. Solo il polo dell’eclittica può dirsi propriamente  non soggetto a variazione, intrepido o immutabile, come in geometria lo è il rapporto della circonferenza al diametro. Infatti il polo celeste è soggetto alla lentissima rivoluzione sul cerchio della precessione.  Se si nega a Parmenide questa conoscenza, quella della precessione,  si deve attribuire a lui la nascita del sistema degli eccentrici e  il progetto di un astrolabio.  Melisso come comandante della flotta contro Atene, esperto di astronomia nautica, poteva ben essere interessato alla scuola di Parmenide anche per questi risvolti.

 

Nel Fr.8 viene detto riferito a to eon, con una terminologia tutta parmenidea di sapore geometrico

 

                              v. 29 il medesimo in se medesimo rimanendo, secondo se stesso giace

VIII, 29 taétñn t' ¤n taétÇi te m¡non kay' ¥autñ te keÝtai

 

                Nel Timeo di Platone il cerchio del medesimo designa l’eclittica. Il piano dell’eclittica appartiene alla sfera celeste, sicché i punti sulla sfera celeste, le stelle ad esempio, trovano la loro corrispondenza in punti giacenti sul medesimo piano, individuati dall’intersezione con esso della retta originata dal polo sud e prolungata fino all’astro (Fig. 15). Abbiamo pertanto una corrispondenza biunivoca  che non altera la rappresentazione funzionale, rimane infatti il medesimo in sé medesimo, e ciascun punto giace sul piano secondo  sé stesso, secondo l’ordine della propria caratteristica che lo individua, cioè secondo l’ordine degli angoli.  Se si vuole, si può osservare che l’espressione parmenidea sia fortemente  sintetica e sia stata di difficilissima lettura  finora.

Non tutta la sfera celeste può essere così rappresentata, perché il polo di proiezione si troverebbe all’infinito, tesi seguita da Melisso per to eon, mentre per Parmenide  c’è un limite estremo:

 

Infatti, uguale da ogni parte, in modo uguale sta nei confini.

 (Fr.8,49).

 

 

Nel fr, 4  la dèa invita ad osservare
come le cose distanti siano fermamente presenti alla mente.

 

        Poiché non potresti separare ciò che esiste dal suo essere connesso a ciò che esiste

                                Né quando sia dovunque disperso del tutto secondo ordine

                                Né quando sia raccolto.

leèsse d' ÷mvw Žpeñnta nñvi pareñnta bebaÛvw:
oé gŒr Žpotm®jei tò ¤òn toè ¤ñntow ¦xesyai
oëte skidn‹menon p‹nthi p‹ntvw katŒ kñsmon
oëte sunist‹menon.

 

                Come si può dire che ciò che esiste sia disperso, con l’impiego di un verbo che veniva usato per dire “sul fare dell’alba” con un’espressione che letteralmente suona insieme al Sole disperso? Si vede il chiarore dell’alba con il Sole assente, eppure si sa che c’è.  Se invece ciò che esiste è anche visto assieme al modello, allora diviene sufficientemente chiaro ciò che Parmenide intende dire. La realtà di ciò che esiste, lontana nello spazio e quindi non  attualmente sotto la nostra percezione, è presente alla mente sia quando, secondo un certo ordine, i punti della sfera celeste si trovano proiettati ( dispersi) sul  piano di una circonferenza, il cui raggio tende però all’infinito, sia quando siano rappresentati sulla superficie di una sfera e così sono raccolti, stanno insieme. C’è da domandarsi se il fr. 4 si riferisca  anche ad un ordinamento  temporale (cosmo) degli eventi (noviluni e pleniluni) il cui schema, se prolungato all’infinito, tocca tutti gli eventi nel passato e nel futuro.

  Dalla trigonometria piana si sa che la tangente di  90° è una retta parallela al piano di proiezione e pertanto non può intersecare quel piano. I punti A e B (Fig. 15) del coluro dei solstizi con latitudine sud si trovano proiettati

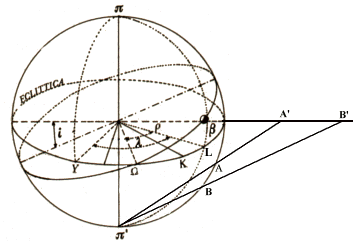
Fig. 15. Esempio di proiezione dei punti del coluro dei solstizi sulla
retta giacente sul pianto di eclittica assunta come piano di proiezione.

sulla retta nei punti A’ e B’. Il polo di proiezione non può mai essere rappresentato sulla retta, perché la retta di proiezione è parallela alla retta in cui giacciono i punti A’ e B’.
L’aver cercato di leggere tutto il Fr. 8 unicamente come una riflessione filosofica sull’essere, e non anche come la descrizione della rappresentazione geometrica della sfera su di un piano passante per l’eclittica o per l’equatore , con un suo linguaggio tutto nuovo, non solo ha impedito la comprensione dell’opera del grande Eleate, ma ha posto un problema, quello dell’ontologia, che si ritrova chiaramente e consapevolmente in Platone e non  in Parmenide.  Con ciò non intendiamo sostenere che il problema filosofico dell’essere sia nato da una incomprensione platonica del linguaggio parmenideo,  avendo trasportato su di un piano diverso da quello parmenideo il linguaggio dell’Eleate. La necessità di compiere un parricidio che sul piano della rappresentazione geometrica dell’universo non avrebbe avuto alcun senso, può forse comprendersi in presenza di conclusioni scettiche tratte dai  sofisti da alcune affermazioni di Parmenide.

La rappresentazione di ciò che esiste è unica e atemporale, possiede tutti i caratteri , tutti i segni che Parmenide attribuisce a ciò che viene significato con to eon.  Così il centro di ciò che si è disvelato in cerchio, accogliendo la suggestione heideggeriana sulla verità come dis-velamento, è sicuramente immobile, e ne viene di conseguenza che è necessario che tutto appaia circolare nell’universo, come pare essere detto negli ultimi due versi del proemio, di difficilissima lettura:

 

ma anche questo apprenderai, come sia necessario che le cose che appaiono

sembrino essere tutte  [circolarmente] circolanti per l'universo.

 

Detto altrimenti la legge del cerchio si impone a tutto ciò che appare nel cielo.

 

L’abbandono dei metodi aritmetici arcaici del pitagorismo si impose e così nacque l’astronomia geometrica greca con i suoi assiomi sulla velocità angolare costante degli astri che si muovono su di un cerchio. L’apparenza dei movimenti irregolari, del movimento anomalistico del Sole sulla sfera celeste ad esempio, potette  facilmente essere spiegata, perché il centro di proiezione non è identico al polo attorno cui tutto appare muoversi. La differenza di modello e apparenza si impose, come si impose al pensiero la forza del modello. L’astronomia matematica greca può dunque raccogliere nella sua storia l’opera del grande Eleate, il cui apporto fu ben superiore a quello di Metone, ricordato per la riforma del calendario, basato sul ciclo di 19 anni.

                Il compito di rileggere tutto il frammento 8 e gli altri alla luce dei risultati e della nuova prospettiva si rende necessario e richiede un confronto con i numerosi studiosi che si sono cimentati con il testo, raccogliendo da loro le preziose osservazioni sul piano filologico, storico e filosofico.

Sul piano dei risultati  conseguiti con la rilettura del proemio c’è innanzi tutto la identificazione della dea del proemio come quella che nell’area del Mediterraneo  è collegata a Sirio. I suoi nomi sono Isthar per la cultura assira babilonese, Inanna per la cultura sumerica e Isis-Sothis per la cultura egizia. In ciò siamo in parte d’accordo con Luigi Ruggiu quando scrive nel suo densissimo commentario filosofico : “Al reale che si manifesta come Essere totale corrisponde sul piano mitico-religioso la forma pre-ellenica del divino della Grande Dea mediterranea che è una e medesima nel molteplice dei nomi e degli aspetti del reale” (17).  Ci allontaniamo però dallo studioso sul piano dell’interpretazione della “Grande Dea mediterranea” perché essa si differenzia sia da Dike e Themis e dalla Daimon, e in generale sulla funzione comunicativa del mito nelle culture arcaiche.

Nelle culture pre-elleniche la dea è in rapporto contemporaneamente ad una stella (Sirio), ad un pianeta (Venere), ad una struttura cosmografica (meridiano del luogo). La questione infatti della “polinomia della Dea” si può affrontare se si sono individuati i molteplici aspetti del reale espressi nei molteplici nomi , espressi appunto nella polinomia.  Ciò che importa però per Parmenide è la relazione che ha la Dea al “cuore immobile della verità ben rotonda” (I,29), nel senso precisamente tecnico che abbiamo mostrato, sicché ad essa si può applicare quanto viene detto della stella-freccia babilonese, ^mullKAK.SI.DI., cioè che “misura la profondità del mare” (18).

L’intuizione che vi sia una corrispondenza di  ciò che esiste, “simile a massa di ben rotonda sfera, a partire dal centro uguale in ogni parte” (Fr.8,43-44) alla Dea, che innanzi tutto rivela “il cuore immobile della verità ben rotonda” (I,29) ci pare essere la tesi più vicina alla nostra lettura, una tesi conseguita con un attento esame delle fonti. Con questa metodologia di lettura però non è possibile andar oltre l’intuizione e mostrare in modo tecnico quella corrispondenza intuita ed affermata, centrale anche per noi per comprendere il testo di Parmenide, per la cui lettura è necessaria, come abbiamo mostrato, anche una competenza  scientifica, congiunta a quella filosofica, filologica e storica.  

Andando oltre Parmenide, si impone ancora la ricerca di tutti i testi composti secondo il sistema delle occorrenze. Le regole di composizione e di comunicazione impiegate nel proemio sono rintracciabili anche in altri testi, non solo greci, essendo questo il sistema arcaico di composizione e di comunicazione che presiede alla formazione del testo letterario. Tale sistema di comunicazione si ritrova nell’opera di Dante, di cui abbiamo riferito due significativi passi,  o nei testi canonici della tradizione religiosa cristiana, di cui abbiamo trattato altrove (19).

Note
(1) MARTIN HEIDEGGER, Parmenide, Adelphi Milano 1999

(2) GIOVANNI FERRERO, La via della Demone. Per lo studio sulla genesi e struttura del poema di Parmenide, in La matematica delle civiltà arcaiche, Torino 1979, pp. 283-321

(3) GIORGIO IMBRAGUGLIA, Via della Demone o via del Nume? In “Filosofia Oggi” anno VIII, Aprile-Giugno 1985 N.2, pp. 233-284.

(4) PARMENIDE, Poema sulla Natura, I frammenti e le testimonianze indirette, Presentazione, Traduzione e Note di GIOVANNI REALE; Saggio Introduttivo e Commentario filosofico di LUIGI RUGGIU, Rusconi, Milano 1991.

(5) MARCO MANILIO, Astronomicon, a cura di Massimo Candellero, Edizioni Arktos – Carmagnola, 1961, pp.126

(6) GIOVANNI FERRERO, Il modello aritmetico della cosmologia arcaica, Appendice a Il secreto dell’arcangelo Gabriele. Ermetismo e cristianesimo nella genesi di Dante secondo il quadro della Sapienza arcaica, in DSU, Rivista del Dipartimento di Scienze dei processi conoscitivi, Anno 1, N. 1. Giugno 1996, pp. 172-182

(7) ANTONIO CAPIZZI, Introduzione a Parmenide, Laterza Bari 1975; La porta di Parmenide. Due saggi per una nuova lettura del poema. Edizioni dell’Ateneo, 1975. Cfr MARGHERITA ISNARDI PARENTE, Parmenide e Socrate demistificati. Questioni di metodo a proposito di alcuni recenti studi di Filosofia antica, in “Rivista critica di Storia della Filosofia” (1976, Fasc. IV) pp. 422-436 e in particolare 424-429.

(8) MARIO NAPOLI, Guida degli scavi di Velia, Di Mauro Editore, 1972, pag.26.

(9) GIOVANNI FERREO, Il sapere di Apollo. La cosmocronologia arcaica secondo il codice iconico narrativo greco, in “Quaderni di Storia della Fisica”, N. 2, 1997, Giornale di Fisica, S.I.F., pp. 3-24

(10) GIOVANNI FERRERO, L’unità del sapere nel quadro della cultura antica. La comunicazione analogica ed iconica del Sapere in Grecia, in “Quaderni di Storia della Fisica” N.4 – 1999, pp. 3-38

(11) LERSCH, Einleitung zur die Chronologie, Aechen 1889, pag. 58, citato da F.K. GINZEL, Spezieller Kanon der Sonnen-und Mondfinsternisse, Berlin 1899, p.267

(12) G.FERRERO, Il sapere di Apollo, op.cit., pp.15-17

(13) M.NAPOLI, op.cit., p.31

(14) M.MANILIO, Astronomicon, op.cit., pp.126-127.

(15) ANDRE’ PARROT, Sumeri, trad. it., Feltrinelli, Milano, 1968, pp.253-282

(16) MELISSO, Testimonianze e frammenti, a cura di Giovanni Reale La Nuova Italia, Firenze 1970 B10 p. 405

(17) PARMENIDE, op.cit., Commentario filosofico al poema di Parmenide “Sulla Natura” di Luigi Ruggiu, pag.167 ; cfr. inoltre pp.183 ssg.

(18) GIORGIO DE SANTILLANA-HERTA VON DECHEND, Sirio centro permanente dell’universo arcaico, in AA.VV., Eternità e Storia. I valori permanenti del divenire storico, Vallecchi editore Firenze, 1970, pag.402

(19) GIOVANNI FERRERO,I CIELI APERTI Il racconto del Battesimo di Gesù di Marco 1,1-13 nel quadro della cultura arcaica in "Atti del Congresso CE.I.S.LO - 1999" Il pensiero forte, arma vincente agli inizi del nuovo millennio Santa Maria La Vite - Olginate 25-26-27 Settembre 1999, Edizioni CE.I.S.LO, Pubblicato con il contributo della Provincia di Lecco, pp.83-109