COSMOLOGIA ARCAICA
Sezione Indiana

Sarasvati, dea della musica, sec.XI, Calcutta
Genesi e struttura algebrica del triangolo di Sarngadeva
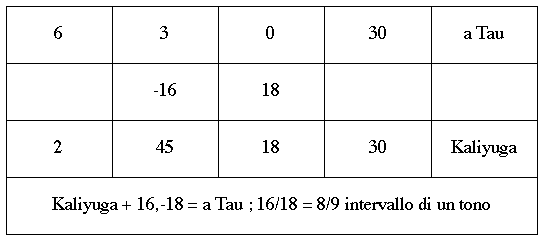
Qui teneremo una procedura algebrica dei termini numerici presenti nel triangolo, richiedendo che venga concesso come conosciute le seguenti informazioni elencate nella tabella

Eccetto la prima linea, tutte le altre sono derivabili dalla tradizione pitagorica e dalla revisione di questa tradizione per determinare il "Giorno di Brahma". Nella prima linea viene indicato che la stella rossa più luminosa della costellazione del Toro cominciò a segnare l'equinozio di primavera, cioè a sorgere con il sole quando i mesi trascorsi dall'origine furono:
Un'ulteriore informazione deve essere richiesta, cioè la differenza temporale tra l'inizio dell'éra Kaliyuga e quella zodiacale del Toro, come da tabella:
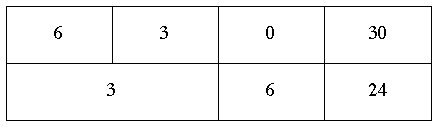
La seconda linea è ottenuta con le seguenti operazioni:
2) Il secondo passo fu quello di porre 3 = 1+2 per ottenere nella seconda linea 4 termini

i cui valori sono tutti: a1= 1*1; a2= 2*1; a3= 3*2*1; a4= 4*3*2*1
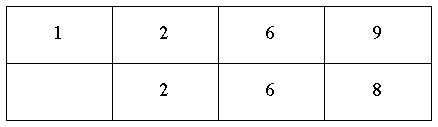
3) Il terzo passo fu quello di vedere nei primi tre numeri l'intervallo di 9/8 trascritto in [6+2+1]/[6+2]
4 Si assuma per la determinazione della differenza dell'anno di 365.25 dall'anno tropico il rapporto di 5/640.
5) Si prendano 9/8 di 640, cioè 720. Anche 720 = 6*5*4*3*2*1
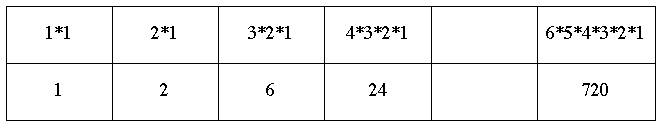
6) Si può vedere che nella quinta cella vi sia 5*24 = 120, essendo 5 l'altro termine della relazione per determinare la differenza chiamata tuono

7) Si ricerchi una quantità determinata dalle operazioni indicate:
2*720+3*120+4*24 = 1896
In questo modo si predispone la tabella ad essere applicata nell'ambito della teoria musicale.
La tabella a questo punto si presenta:
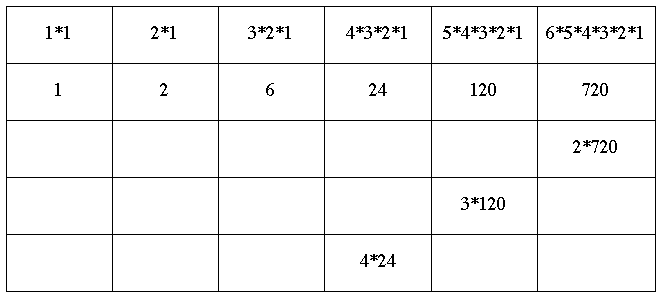
La tabella è impostata ma non completata.
8) Applicando la terza relazione, quella per il Fulmine, si ricerchi il numero degli anni necessari affinchè la differenza anno sidereo e anno tropico sia equivalente a giorni 1896:
Si consideri allora la differenza:
[1896*(352/5)] - [150*(890.5)] = 96+3/5
e si domandi
a) di quanto si deve diminuire (890.5) affinchè la differenza sia prossima a 72 anni? Considerando che 150/6 = 25 si vedrà che si dovrà diminuire 890.5 di 1/6, sicchè si avrà

9) Si assuma come base del ciclo 6*720 anni e si ricerchi il numero dei mesi
10) Il rapporto per determinare il periodo sinodico della luna è dato da
Si confronti la forma di questa equivalenza con quella del punto 8). In questa 150 è il fattore, mentre qui è il divisore della medesima quantità.
11) La tabella ora può essere completata, inserendo nelle celle opportune i termini mancanti
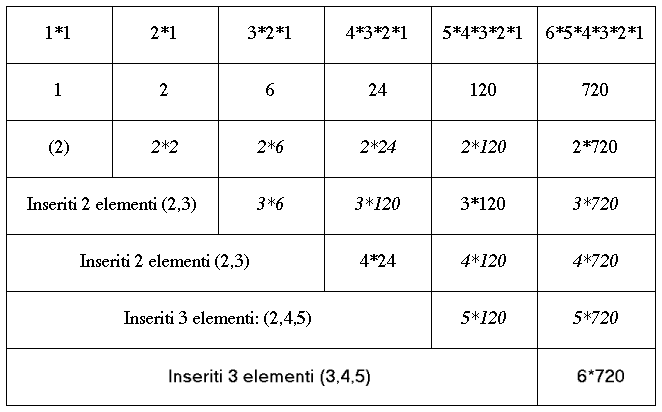
Le condizioni date permettono pertanto di calcolare sia il numero dei giorni per l'anno tropico
sia il numero dei mesi, essendo il periodo sinodico della luna dato da
Il problema dunque che Sarngadeva ha affrontato
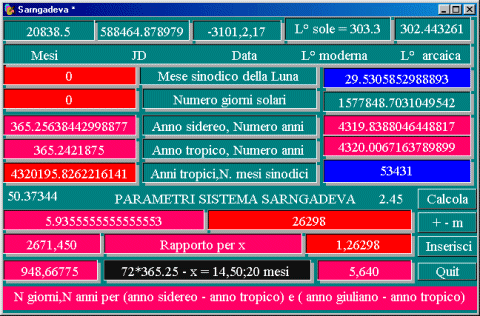 redigendo la tabella triangolare riguarda la determinazione dei tre rapporti che strutturano tutta quanta la Cosmologia arcaica, mutando i periodi lunari e quelli solari, cominciando dalla sequenza che determina l'inizio dell'Éra del Toro. L'aver predisposto poi una corrispondenza tra tale tabella e i numeri in essi presenti e l'organizzazione della scala e il problema di assegnare un numero univoco a ogni possibile permutazione delle note della scala, ha semplicemente nascosto la "miniera di gemme" che è l' "Oceano della musica".
redigendo la tabella triangolare riguarda la determinazione dei tre rapporti che strutturano tutta quanta la Cosmologia arcaica, mutando i periodi lunari e quelli solari, cominciando dalla sequenza che determina l'inizio dell'Éra del Toro. L'aver predisposto poi una corrispondenza tra tale tabella e i numeri in essi presenti e l'organizzazione della scala e il problema di assegnare un numero univoco a ogni possibile permutazione delle note della scala, ha semplicemente nascosto la "miniera di gemme" che è l' "Oceano della musica".
Nel sito di Dwight William Johnson, tecnicamente accurato per il calcolo astronomico e per l'analisi del sistema indù,
Exegesis of Hindu Cosmological Time Cycles viene data una tabella di confronto tra i parametri della cosmologia indù e quelli che l'astronomo Newcomb calcolò per il 1 gennaio 1900 d.C.

© 2001 Proprietà letteraria riservata