COSMOLOGIA ARCAICA
Sezione Indiana
Il triangolo di Sarngadeva

Il prof. Giovanni Piana (Filosofia teoretica, studioso di storia delle teorie musicali e di Filosofia della musica,Università di Milano,), presenta e commenta un testo indiano del XIII secolo, di cui qui trascriviamo l'inizio per le informazioni storiche, necessarie per un'ipotesi di lettura cosmologica del cosiddetto triangolo di Sarngadeva.
-
Da Sarngadeva's Triangle.htm trascriviamo:
Nel trattato intitolato Oceano della musica (Sangitaratnakara) [1]uno dei più importanti testi classici della tradizione teorico-musicale indiana, Sarngadeva propone un’interessante digressione matematica sulla quale ci vogliamo anzitutto soffermare[2].
Nella sezione quarta del capitolo primo [3] Sarngadeva si propone raccogliere in una un’unità tutte le permutazioni possibili delle sette note della scala sagrama illustrando anche un metodo pratico per il loro completo dominio. Precisamente si tratta di realizzare una duplice operazione: da un lato, ad ogni permutazione deve poter essere associato un numero, dall’altro deve essere possibile«estrarre» da un determinato numero - ovviamente compreso tra 1 e il numero massimo di permutazioni possibili - la permutazione ad esso associato.
[1] Sarngadeva, Sangitaratnakara, testo sanscrito e traduzione inglese di R. K. Shringy, vol. I, Varanasi 1978, p. 208. Talora il titolo viene reso con Oceano di gemme della musica. «Ratnakara» può essere tradotto con «mare, oceano» ; oppure con «miniera di gemme» (jewel-mine, sea, ocean M. Monier-Williams, A Sanskrit-English Dictionary, Oxford 1899 (1990)) - Sono debitore di molti stimoli per l’argomento di questo saggio, oltre che di un concreto aiuto bibliografico, a Francesca Dell’Acqua, che ha svolto nel 1994-95 una tesi di laurea intitolata «Teorie della musica e filosofia nel Sangitaratnakara di Sarngadeva» presso l’insegnamento di Filosofia Teoretica da me tenuto, con correlazione di Carlo Della Casa. - Una stesura preparatoria di questo lavoro è stata presentata al convegno organizzato dal Seminario Permanente di Filosofia della musica, Dipartimento di Filosofia dell’Università degli Studi di Milano, svoltosi a Gargnano, Palazzo Feltrinelli, 29 settembre-1 ottobre 1997.
[2]. Siamo nel XIII secolo, in un’epoca che viene considerata di transizione tra la musica antica e la musica medioevale. M. R. Gautam propone di distinguere la storia della musica indiana in tre grandi fasi, la musica antica, medioevale e moderna. Le prime due possono essere considerate come concluse approssimativamente nel XIII secolo e nel XVIII secolo, mentre la terza arriva ai nostri giorni. M. R. Gautam, Evolution of Raga and Tala in Indian Music, New Delhi 1993, p. IX. Sarngadeva viene trattato nel cap. IV, pp. 61 sgg.
[3] Sangitaratnakara, 63c-71, cit. p. 208-220.
Lettura cosmologica
-
È rilevante per una lettura cosmologica del triangolo di Sarngadeva, presente nel testo Oceano della musica e della danza, come altri ancora traducono il titolo, sia la notizia che il testo è del XIII secolo, (alcuni pongono la vita del teorico indiano della musica dal 1210 al 1247) sia la regola di formazione della matrice numerica. L'autore operò nel Deccan, nell'India centrale meridionale, prima che la regione fosse conquistata dai Mussulmani, mentre nell'India del Nord si instaurava la dinastia dei Mamelucchi (1206-90). Questo permette di affermare che l'autore riporta la tradizione musicale indiana prima dell'influenza sulla musica da parte della cultura musicale mussulmana.
- L'intervallo DT = 20,42,58 m
- la data è: 1243,12,28
- (25-6),0,25+2 mesi
- L° Polare = - 6151 mesi oppure che
- per DT= 6151 mesi L° Polare = 0°
- (20,42,58) - (2,8,6) = 18,34,52 mesi = 66892 mesi
- 16,26,46 mesi, che corrisponde al 27 febbraio 1 d.C., cioè
- DT = 16,42,39 m
- data: 78,3,17 cioè il primo plenilunio dell'antica éra indù Saka.
- Di quale stella è possibile scrivere la seguente sequenza, tenendo presente la sequenza 2,6,25 e quella precedentemente scritta (25-6,0,25+2) per la Polare?
- 25-6,6,0 mesi
- Si tratta di Sirio, di quella stella che fu, a detta di Herta von Dechend e di Giorgio de Santillana, il centro dell'universo arcaico e tutte le culture hanno diversi e interessanti racconti a suo riguardo. Non è qui il caso di ricercare sotto quali nomi essa sia stata celebrata e venerata.
- Con una semplice differenza [(19,6,0) - (16,42,39)] si può trovare che la longitudine di Sirio al tempo zero era di
- 2,23,21 mesi.
Nella mitologia indo-ariana il ruolo dei Gemelli è costante e rilevante ed è stato studiato da G. Dumézil (Le roman des jumeaux,Esquisses de mythologie, nrf Gallimard 1994). Possiamo allora domandare in quale tempo Castore, cioè alpha Geminorum misura in gradi la longitudine espressa in mesi diDT = 6,25,2 mesi una misura ottenuta dalla permutazione (circolare) del valore iniziale, 2,6,25:
La risposta si trova nella seguente espressione, con permutazione sequenza originaria:(2+1),- (25-1), -(6+2+1) mesi che implica che al tempo zero posto nella costellazione dei Gemelli tra h e m Geminorun,
alpha Geminorum = 11,27,33 mesi una misura rilevante, perchè, tra l'altro, la circonferenza di 43200 unità ha come diametro 13.751 unità.
Il quadro sinottico del percorso di lettura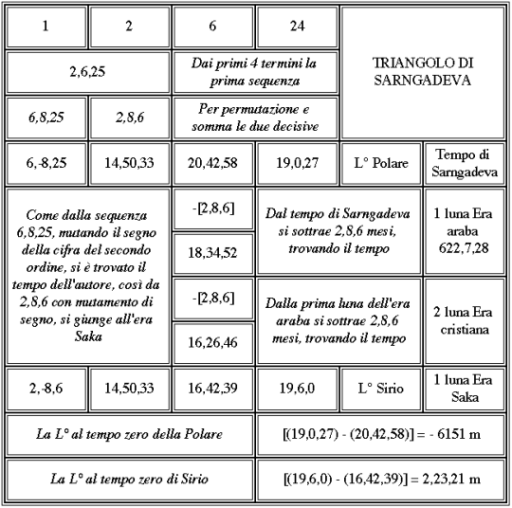 con i riferimenti uranografici trovati (Polare,Sirio) e le tre ere, quella indù, quella araba e quella cristiana, mostrano non solo la possibilità che il triangolo di Sarngadeva avesse una funzione memorizzatrice nell'ambito del sapere astronomico, secondo uno schema di lettura e di calcolo, solo in minima parte mostrato, ma anche una sua specificità nel basarsi sul ciclo lunisolare di 4320 anni
siderei.
con i riferimenti uranografici trovati (Polare,Sirio) e le tre ere, quella indù, quella araba e quella cristiana, mostrano non solo la possibilità che il triangolo di Sarngadeva avesse una funzione memorizzatrice nell'ambito del sapere astronomico, secondo uno schema di lettura e di calcolo, solo in minima parte mostrato, ma anche una sua specificità nel basarsi sul ciclo lunisolare di 4320 anni
siderei.
Infatti si ha ancora una sorpresa se si va a cercare la situazione planetaria al primo plenilunio dell'era araba, rappresentata dalla seguente mappa elaborata al computer dal programma Voyager II per il sistema Macintosh.
Senza questo programma sarebbe stato ben difficile trovare questo ulteriore riscontro, tuttavia ci pare che esso rappresenti una delle ragioni per accettare un sistema basato sul ciclo di 4320 anni per memorizzare e comunicare le informazioni sulle Ere e sulle stelle.
L'apparente regola di formazione è molto semplice: la prima linea contiene sei celle con il fattoriale di 1 a 6. Per fattoriale di un numero (n!) si intende il numero che si ottiene dalla moltiplicazione di tutti i numeri in senso decrescente, da n a 1 e tale numero designa le permutazioni possibili di n oggetti presi uno ad uno. Le altre linee del triangolo si ottengono mediante la moltiplicazione per 2,3,4,5,6 come si trova nella seguente matrice:
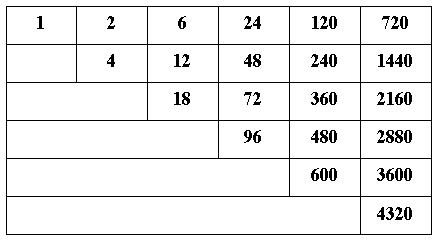
Di fronte a questo insieme numerico, prima di procedere a qualsiasi ipotesi di lettura, è necessario individuare il termine numerico consistente nell'ambito cosmologico-astronomico.
Se 4320, che si presenta isolato, è stato ottenuto dalla moltiplicazione per 6 di 720, si può subito vedere che esso equivale a 60 per 72 e designerebbe pertanto, nell'ipotesi di una lettura cosmologica, il numero necessario di anni per un arco del polo celeste attorno al polo dell'eclittica di 60° o, in altri termini, per un arco di precessione degli equinozi di 60°. Non è sufficiente aver osservato tale equivalenza per affermare che il triangolo numerico ha anche una lettura cosmologica-astronomica, se non si sa ottenere i parametri di un ciclo lunisolare basato su 4320 anni e mostrare che tali parametri sono derivabili immediatamente dalla matrice.
A proposito di 4320 anni, si può ricordare che il Bhagavad-gita riporta che il giorno di Brahma dura 4.320 000 000 anni solari, un periodo multiplo di 1.000.000 di volte.
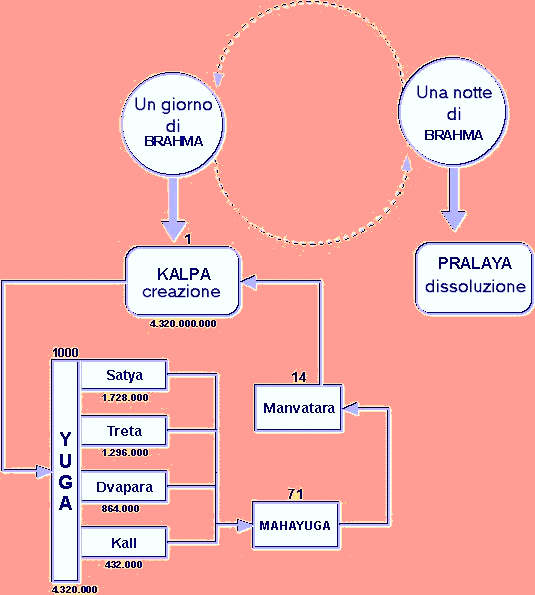 Inoltre l'ultima era, corrispondente all'era attuale, cominciata il 17-18 febbraio 3102 A.C., il Kali-yuga, dura 432000 anni, mentre le altre precedenti ere sono rispettivamente di 1.728.000 anni, di 1.2960.00 e di 864.000 anni, come sono indicate nello schema.
Inoltre l'ultima era, corrispondente all'era attuale, cominciata il 17-18 febbraio 3102 A.C., il Kali-yuga, dura 432000 anni, mentre le altre precedenti ere sono rispettivamente di 1.728.000 anni, di 1.2960.00 e di 864.000 anni, come sono indicate nello schema.Ora la suddivisione dei 4 periodi è semplicemte 100 volte i primi quattro numeri che costituiscono la tetraktys pitagorica. Sicché il ciclo vero e proprio è solo di 43200 anni (tropici), dieci volte il ciclo di 4320 anni, indicato nell'ultima cella della sesta colonna del triangolo di Sarngadeva.
Su questo aspetto sarà necessario ritornare in una pagina dedicata a tale tema e mostrare come il sistema presente nello schema possa essere una correzione del sistema pitagorico, riguardante la misura annuale della precessione degli equinozi. Non più 1° ogni 72 anni, ma ogni 71 + x/14 anni essendo il ciclo suddiviso in 14 Manvatara.
Alla base della cosmologia arcaica,per il calcolo delle longitudini del sole alle lune nuove (congiunzioni) e alle lune piene (opposizioni), c'è un modello (presente nel Sistema A) ben conosciuto dagli studiosi (Kugler, Neugebauer, ...) dell'astronomia babilonese.
 Esso si basa sulla suddivisione del percorso apparente del sole sulla sfera delle stelle fisse nel sistema geocentrico in due archi lungo i quali il sole presenta nel tempo di una lunazione incrementi angolari costanti. Vi sono pertanto due punti di discontinuità e due velocità angolari e due archi. Il rapporto tra le due velocità, a volte, è pari al rapporto di un intervallo musicale (generalmente un semitono). Questo aspetto lega l'astronomia alla teoria musicale.
Esso si basa sulla suddivisione del percorso apparente del sole sulla sfera delle stelle fisse nel sistema geocentrico in due archi lungo i quali il sole presenta nel tempo di una lunazione incrementi angolari costanti. Vi sono pertanto due punti di discontinuità e due velocità angolari e due archi. Il rapporto tra le due velocità, a volte, è pari al rapporto di un intervallo musicale (generalmente un semitono). Questo aspetto lega l'astronomia alla teoria musicale.
Quale linea e quale colonna deve essere presa in esame? Il termine numerico 4320 si trova alla sesta colonna e non deve più comparire. Sulla base di questa ragione si è formata la seguente linea e colonna:



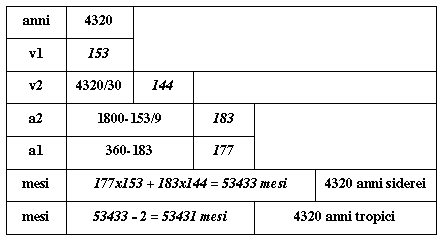 Poiché in 4320 anni la differenza tra l'anno sidereo e l'anno tropico ammonta a più di 60 giorni, a poco più dunque di due mesi lunari, 4320 anni tropici corrispondono a 53431 mesi lunari.
Poiché in 4320 anni la differenza tra l'anno sidereo e l'anno tropico ammonta a più di 60 giorni, a poco più dunque di due mesi lunari, 4320 anni tropici corrispondono a 53431 mesi lunari.A questi risultati non saremmo giunti se non avessimo ottenuto dalla prima linea e dalla quinta colonna i valori di 153 e 1800, che assieme a 4320 permettono di individuare i parametri del sistema. Infatti 4320 diviso per 30, essendo 30°/m l'incremento del sole per lunazione sull'arco lungo, fornisce il termine minore del rapporto tra le due velocità, cioè 144. La procedura seguita è indicata dalla seguente tabella sinottica per i parametri del ciclo lunisolare di 4320 anni solari.
Benché possa apparire comprovata la lettura cosmologica del triangolo di Sarngadeva, tuttavia essa non è sufficiente, perchè non si è ancora trovato il significato storico di questo documento e nemmeno la sua determinazione algebrica nell'ambito del sapere cosmologico e cronologico. In caso contrario sarebbe solo un gioco intellettuale, mentre tutti i documenti della cultura arcaica permettono di accedere ad una conoscenza storica, ad una datazione. È proprio della cultura arcaica non separare teoria e applicazione, ma di presentare le regole mediante la esemplificazione paradigmatica, nel racconto o nella struttura dell'icona, di un evento.
Anche se si trovasse che nella teoria degli intervalli musicali sia impiegato il semitono di 17/16, a cui si riduce il rapporto 153/144 del ciclo lunisolare di 4320 anni, non avremmo ancora la prova che il documento abbia un significato astronomico-cosmologico.
Il ciclo di 4320 anni lega gli anni del XIII secolo a quelli del 3000 a. C., anni in cui alfa Tauri segnò l'equinozio di primavera e secondo la cultura indù iniziò l'era di Kalí, le cui dense tenebre oscurano la visione degli uomini.
Ricorrendo alla prima tabella con le prime quattro celle della prima linea, dovremmo individuare una successione di intervalli temporali in mesi lunari, in base al quale ottenere informazioni rilevanti.
Il triangolo di Sarngadeva è il triangolo delle permutazioni, presentato dall'autore "per tutte le permutazioni possibili delle sette note della scala sagrama (G.Piana)". In questa ricerca, per non cadere nella sovradeterminazione della interpretazione si dovrà vedere una succesione di permutazioni

Sapendo che il tempo iniziale si trova al plenilunio di primavera del 4787 a.C., si scriva la seguente sequenza:
Ciò che importa è trovare intervalli temporali per eventi che hanno rilievo per le diverse culture, che si affrontavano nel XIII secolo in India, quella indù e quella islamica.
Dalla sequenza originaria (2,6,25) si scriva con permutazione e somma:
2,6+2,6
Si assuma la prima sequenza, mutando il segno al secondo posto, (6,-8,25) e ad essa si aggiunga l'intervallo del ciclo lunisolare di 4320 anni siderei, cioè 53433 = 14,50,33 mesi e si calcoli la data del plenilunio individuato:
Al novilunio successivo il sole si trova in Capricorno. In occasione del passaggio del sole nella costellazione del Capricorno ricorre la festa religiosa indù di particolare importanza, la Makara-samkranti, ed è occasione di un grande raduno alla foce del Gange (Ganga-sagara-mela)
Siamo pertanto al tempo di Sarngadeva. Il cielo ruota attorno ad una stella, chiamata Polare (alpha Ursae Minoris), che non è più quella di 4320 anni prima. La sua longitudine ricavabile dalla sequenza originaria (2,6,25) è
Se da questo intervallo andiamo indietro nel tempo di 2,8,6 mesi, (il secondo intervallo derivato dalla prima sequenza trovata) cioè operiamo una sottrazione, troviamo l'intervallo:
Se torniamo indietro nel tempo della medesima quantità, sottraendo a 18,34,52 l'intervallo di 2,8,6, si giunge all'intervallo:
Si muti il segno al secondo valore della sequenza 2,8,6, operando in modo analogo alla sequenza 6,8,25.
A 2,-8,6 si aggiunga l'intervallo del ciclo lunisolare di 4320 anni siderei, cioè 53433 = 14,50,33 mesi e si calcoli la data del plenilunio individuato:
È attestata nel Panca Siddantika di Varaha Mihira, del VI sec. d.C. il riferimento a all'Èra Saka.

-
La tabella seguente mostra come il riferimento al sistema del ciclo di 4320 anni
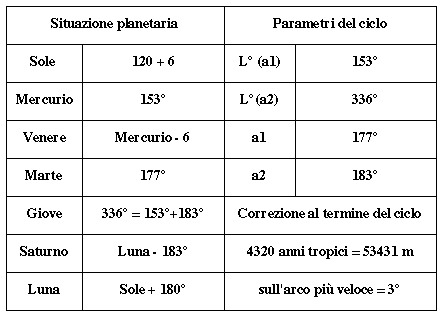 sia finalizzato a comunicare anche la situazione planetaria di un plenilunio che segna il tempo di un evento, la cui importanza nella storia dell'India è indubbia. Dal tempo di questo evento è possibile risalire
all'inizio del Kali-yuga mediante il ciclo di 4320 anni.
sia finalizzato a comunicare anche la situazione planetaria di un plenilunio che segna il tempo di un evento, la cui importanza nella storia dell'India è indubbia. Dal tempo di questo evento è possibile risalire
all'inizio del Kali-yuga mediante il ciclo di 4320 anni.
Come era da aspettarsi, il triangolo di Sarngadeva non è un semplice gioco intellettuale su basi matematiche, ma è un documento storico che riflette la coscienza della cultura indù, presente nell'India centrale meridionale, quando l'islamizzazione dell'India del Nord si faceva possibile e la estensione delle conoscenze che l'alta cultura religiosa deve avere per potere dialogare e comprendere altre culture.
Nella vita di Sri Caitanya Mahaprabhu (nato il 18 febbraio 1486), ad esempio, si narra di una sua conversazione con il Cadì di Navadvipa sul Corano e sugli sastra vedici. Conversazioni analoghe forse erano più frequenti di quanto oggi siamo disposti ad ammettere, come erano frequeni nella Toledo medioevale le conversazioni tra gli islamici, i cristiani e gli ebrei, sapendo allora ciascuno quale fosse la tradizione dell'interlocutore.
Per informazioni sugli antichi calendari indiani si vada al sito Via Lattea mentre per le notizie storiche si vada alle ere e i calendari.
© 2001 Proprietà letteraria riservata