Simboli

Simboli - Operazioni - Numeri


Simboli operazionali

Per trovare i parametri del ciclo lunisolare di Apollo è necessario operare sui numeri posti accanto al simbolo della moltiplicazione e della divisione, mentre il simbolo simile al quadrifoglio occorre per determinare il ciclo legato al cervo.

Operazioni



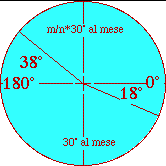
Operazioni

Moltiplica per 10 10,10+11+30 e dividi per 30.
Si ottiene 217 il parametro m e il numero degli anni solari, 10*60 +51 = 651.
Si osservi che il parametro m deriva da A/30 con A = il numero degli anni tropici del ciclo.Per questo è necessario moltiplicare per 10 il numero 651 per ottenere un numero intero. Al termine di questo percorso di lettura ci si trova nello spazio del riquadro dietro la figura femminile della dèa, tra una spirale ad S con i due cerchiolini della decina, in alto, e l'indicazione di un termine numerico designato dalla trentina e dalla decina , in baso.

Spirale ad S indicante l'operazione 180° + 20° e 180° - 20° e i simboli numerici della decina - cerchio con punto centrale - e della trentina - la linguetta.
Ora per risolvere l'equazione con B = mesi lunari e con a la lunghezza dell'arco solare più corto

B - 360*217/10 = [n-217]*a

è necessario individuare sia il valore dell'arco minore a, sia il valore di n. Il valore dell'arco non viene esibito nel riquadro. Infatti è più semplice indicare la differenza rispetto a 180° di due archi piuttosto che scrivere i due valori.Essi sono simmetrici rispetto alla metà dell'angolo giro. Il significante iconico di questa simmetria è dato dalla simmetria della spirale ad S, mentre le due decine indicano insieme la misura della differenza. I due archi saranno pertanto 160° e 200°, il cui rapporto è pari a quello di un intervallo musicale, precisamente a quello di terza maggiore: 4/5. L'equazione diviene

10*B - 360*217 = [n-217]*a

I due membri sono entrambi due equazioni con due incognite, l'una in B, numero di mesi lunari corrispondenti a 651 anni, e, l'altra, in n, il termine maggiore del rapporto tra le due velocità del carro solare sui due archi. Il valore di entrambe le due equazioni si legge direttamente nell'accostamento del grafema della linguetta con quello del cerchio con punto centrale. Il suo valore numerico non è 40, ma in notazione sessagesimale, 40,0; = 40*60.
10*B - 360*217 = [n-217]*160 = 2400

Allora B = 8052 mesi e n = 232. Tutti i parametri fondamentali del sistema di guida del carro solare legato ad Apollo, raffigurato nel riquadro dell'anfora di Milo sono determinati (A = 651 anni; B = 8052 mesi lunari; a1 = 160° e a2 = 200°; m/n = 217/232).

Il sistema di Apollo

Mancano per la completa determinazione del sistema, il valore di altri due parametri: la longitudie dell'inizio dell'arco lento e la correzione finale al termine del ciclo di 651 anni.
Nel riquadro non v'è alcun significante rispetto al concetto astratto di correzione, termine che si ritrova unicamente in Anassimandro, ma due palmette poste tra le zampe dei cavalli. La domanda allora nel contesto iconico del riquadro è la seguente: Quanto devono ancora percorre i cavalli, 651 anni dopo l'evento raffigurato nel riquadro, quando il carro solare si trovava a 18° 7'? Una prima risposta a questa domanda si trova nella palmetta di sette petali, dalla parte di Apollo, e in quella di sei, dalla parte di Artemide. La correzione al termine del ciclo DL°1 , quella sull'arco lento, sarà in prima lettura di 7°. Da un punto di vista della cosmocronologia della cultura arcaica questo ulteriore incremento, DL°1, in base al quale è possibile scrivere
L°(8052) = L°(0) + DL°1

se si è sull'arco lento, oppure
L°(8052) = L°(0) + 232/217*DL°1

se si è sull'arco veloce, non è una correzione empirica dovuta ad osservazioni e misurazioni, ma dipende dal calcolo dell'anno tropico, espresso in giorni, e da quello del mese lunare espresso sempre in giorni. Se con At e con Ms, vengono designati i periodi dell'anno tropico e del mese sinodico medio della luna, allora la differenza in giorni
B*Mt - A*At

fornisce in gradi la correzione finale al termine del ciclo sull'arco veloce dell'eclittica, su quell'arco lungo il quale il carro solare procede ad incrementi di 30° al mese, procede con quella velocità del modello originario definito dalle due assunzioni di base:
1) che il sole percorra ogni giorno un grado;
2) che il mese lunare sia esattamente di 30 giorni. Applicando la formula precedente, la correzione sull'arco lento per il ciclo di Apollo è:
7° (7+6)' (7+4)"


Disegnata nello spazio centrale tra le zampe dei cavalli si trova una spirale ad S con otto palmette, cui è associato il grafema della decina, un cerchio con punto centrale. Il valore numerico - 18 - che si ottiene dalla somma degli elementi, combinato con il significante della spirale ad S, suggerisce il dato in base al quale calcolare la longitudine dell'inizio dell'arco lento, a1: 18° gradi prima del punto vernale, cioè 360° - 18° = 342°. L'arco lento inizia a L° 342° e termina a L° 142°. L'arco veloce inizia a L° 142° e termina a L° 342°.

Sintassi della comunicazione Parmenide
© 1996 Proprietà letteraria riservata